
分析 (Ⅰ)判断数列{an}是等比数列,设公比为q,利用a1=2,8a4=a7.求出公比,即可得到通项公式.
(Ⅱ)由(Ⅰ),化简${b_n}=\frac{a_n}{{n({n+1}){2^n}}}({n∈{N^*}})$,利用裂项法求解数列的和即可.
解答 解:(Ⅰ)由题,${a_{n+2}}{a_n}={a_{n+1}}^2({n∈{N^*}})$,所以,数列{an}是等比数列,…(2分)
设公比为q,又a1=2,$8{a_4}={a_7}⇒8{a_1}{q^3}={a_1}{q^6}⇒q=2$,…(4分)
所以,${a_n}={a_1}{q^{n-1}}={2^n}({n∈{N^*}})$…(6分)
(Ⅱ)由(Ⅰ),${a_n}={2^n}$,${b_n}=\frac{a_n}{{n({n+1}){2^n}}}=\frac{1}{{n({n+1})}}=\frac{1}{n}-\frac{1}{n+1}$,…(9分)
数列{bn}的前n项和Sn=a1+a2+…+an=$({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+…+({\frac{1}{n}-\frac{1}{n+1}})$=$1-\frac{1}{n+1}=\frac{n}{n+1}$.…(12分)
点评 本题考查等比数列的判断,裂项法求解数列的和,考查分析问题解决问题的能力.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
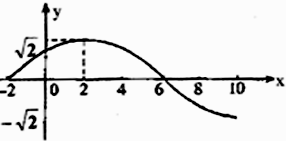 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 965 | B. | 975 | C. | 985 | D. | 995 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com