
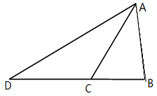
 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长. 分析 利用余弦定理,求出∠ACB=60°,∠ACD=120°,在△ACD中,AC=10,∠ADB=30°,∠ACD=120°,利用正弦定理可得结论.
解答 解:在△ABC中,AB=10,AC=14,BC=6,
由余弦定理得$cos∠ACB=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2AC•BC}=\frac{100+36-76}{2×10×6}=\frac{1}{2}$,
所以∠ACB=60°,∠ACD=120°,
在△ACD中,AC=10,∠ADB=30°,∠ACD=120°,…8分
由正弦定理得,$\frac{AC}{sin∠ADB}=\frac{AD}{sin∠ACB}$
所以$AD=\frac{AC•sin∠ACB}{sin∠ADB}=\frac{{10•sin{{120}°}}}{{sin{{30}°}}}=10\sqrt{3}$…12分.
点评 本题考查正弦、余弦定理的运用,考查学生的计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
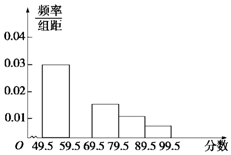 在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
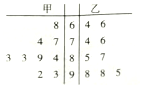
| A. | 甲的中位数是89,乙的中位数是98 | |
| B. | 甲的各科成绩比乙各科成绩稳定 | |
| C. | 甲的众数是89,乙的众数是98 | |
| D. | 甲、乙二人的各科成绩的平均分不相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com