
分析 (1)令f(-x)=-f(x)得出关于x的方程,根据判别式证明方程有解即可;
(2)令f(-x)=-f(x)得出关于x的方程,令t=2x得出b关于t的函数g(t),求出函数g(t)在[$\frac{1}{2}$,2]上的值域即可;
(3)令f(-x)=-f(x)得出关于x的方程,令2x+2-x=t得出关于t的一元二次方程在[2,+∞)上有解,根据二次函数的性质不等式方程组求出m的范围.
解答 解:(1)证明:∵f(x)=ax2+x-a,∴f(-x)=ax2-x-a,
令f(-x)=-f(x)得ax2-x-a=-ax2-x+a,化简得ax2-a=0(a≠0),
∵△=4a2>0恒成立,
∴方程f(-x)=-f(x)必定有解,即函数f(x)=ax2+x-a必有局部对称点.
(2)f(x)=2x+b,f(-x)=2-x+b,
令f(-x)=-f(x)得2x+2-x=-2b,即b=-$\frac{1}{2}$(2x+2-x),
令2x=t,g(t)=-$\frac{1}{2}$(t+$\frac{1}{t}$),∵x∈[-1,1],∴$t∈[{\frac{1}{2},2}]$,
∴g′(t)=-$\frac{1}{2}$+$\frac{1}{2{t}^{2}}$,令g′(t)=0得t=1或t=-1(舍).
当$\frac{1}{2}$≤t<1时,g′(t)>0,当1<t≤2时,g′(t)<0,
∴g(t)在[$\frac{1}{2}$,1]上单调递增,在(1,2]单调递减,
∵g($\frac{1}{2}$)=-$\frac{5}{4}$,g(1)=-1,g(2)=-$\frac{5}{4}$,
∴g(t)的最大值为-1,g(t)的最小值为-$\frac{5}{4}$.
∴b的取值范围是$[{-\frac{5}{4},-1}]$.
(3)f(x)=4x-m•2x+1+m2-3,f(-x)=4-x-m•2-x+1+m2-3,
令f(-x)=-f(x)得4x+4-x-2m(2x+2-x)+2(m2-3)=0(*),
∵f(x)=4x-m•2x+1+m2-3在R上有局部对称点,
∴4x+4-x-2m(2x+2-x)+2(m2-3)=0在R上有解.
令2x+2-x=t,则t∈[2,+∞),4x+4-x=t2-2,
∴关于t的方程t2-2mt+2m2-8=0在t∈[2,+∞)上有解,
令h(t)=t2-2mt+2m2-8,则h(2)=2m2-4m-4≤0或$\left\{\begin{array}{l}{△=4{m}^{2}-4(2{m}^{2}-8)≥0}\\{m≥2}\\{h(2)=2{m}^{2}-4m-4>0}\end{array}\right.$.
解得:$1-\sqrt{3}≤m≤1+\sqrt{3}$或$1+\sqrt{3}<m≤2\sqrt{2}$,即1-$\sqrt{3}$≤m≤2$\sqrt{2}$.
∴m的取值范围是[1-$\sqrt{3}$,2$\sqrt{2}$].
点评 本题考查了对新定义的理解,函数最值的计算,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
 为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
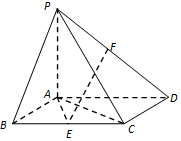 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | C. | $-\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com