
分析 (1)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值点即可.
解答 解:(1)f(x)的定义域为(0,+∞).
当a=3时,$f(x)=(x+1)lnx-3(x-1),f'(x)=lnx+\frac{1}{x}-2$,
f'(1)=-1,f(1)=0.
所以曲线y=f(x)在(1,f(1))处的切线方程为x+y-1=0.
(2)$g(x)=lnx-a\frac{x-1}{x+1}$,x>0,a>1,
$g'(x)=\frac{{{x^2}+2(1-a)x+1}}{{x{{({x^2}+1)}^2}}}$,
令F(x)=x2+2(1-a)x+1,其对称轴为x=a-1>0,△=4a(a-2)
①当△≤0,即1<a≤2,F(x)≥0,g'(x)≥0,
g(x)在(0,+∞)单调递增,无极值.
②当△>0,即a>2,
令g'(x)>0,则$0<x<a-1-\sqrt{a(a-2)}或x>a-1+\sqrt{a(a-2)}$,
令g'(x)<0,则$a-1-\sqrt{a(a-2)}<x<a-1+\sqrt{a(a-2)}$
所以,增区间为$({0,a-1-\sqrt{a(a-2)}})和({a-1+\sqrt{a(a-2)},+∞})$
减区间为$({a-1-\sqrt{a(a-2)},a-1+\sqrt{a(a-2)}})$
所以,极大值点是$a-1-\sqrt{a(a-2)}$,极小值点是$a-1+\sqrt{a(a-2)}$
综上:当1<a≤2时,f(x)在(0,+∞)单调递增,无极值.
当a>2时,f(x)在$({0,a-1-\sqrt{a(a-2)}})和({a-1+\sqrt{a(a-2)},+∞})$上单调递增,
在$({a-1-\sqrt{a(a-2)},a-1+\sqrt{a(a-2)}})$上单调递减;
极大值点是$a-1-\sqrt{a(a-2)}$,极小值点是$a-1+\sqrt{a(a-2)}$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及切线方程问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
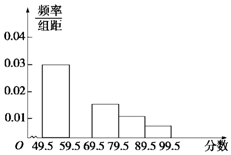 在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com