
| A�� | $\left.\begin{array}{l}���ͦ�\\ m�ͦ�\end{array}\right\}⇒m�Φ�$ | B�� | $\left.\begin{array}{l}���ͦ�\\ m?��\end{array}\right\}⇒m�ͦ�$ | C�� | $\left.\begin{array}{l}m�Φ�\\ m�Φ�\end{array}\right\}⇒���Φ�$ | D�� | $\left.\begin{array}{l}���Φ�\\ m?��\end{array}\right\}⇒m�Φ�$ |
���� ����ƽ����ƽ��ƽ�С���ֱ�����ʣ����洹ֱ�����ʼ�����ƽ�к����洹ֱ���ж����������Ƕ���Ŀ�е��ĸ�����һ���з��������ɵõ���ȷ�Ľ��ۣ�
��� �⣺����A����$\left\{\begin{array}{l}{���ͦ�}\\{m�ͦ�}\end{array}\right.$⇒m�Φ���m?�����ʴ���
����B����$\left\{\begin{array}{l}{���ͦ�}\\{m?��}\end{array}\right.$����m��²�һ����ֱ������ͼ��ʾ�����ʴ�
����C����$\left\{\begin{array}{l}{m�Φ�}\\{m�Φ�}\end{array}\right.$��������²�һ��ƽ�У�����ͼ��ʾ�����ʴ���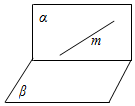
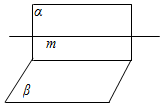
����D����$\left\{\begin{array}{l}{���Φ�}\\{m?��}\end{array}\right.$⇒m�Φ£���������ƽ�е����ʣ����ж�D��ȷ��
��ѡ��D
���� ���⿼���֪ʶ���ǿռ���ֱ����ƽ��֮���λ�ù�ϵ���������տռ�����֮���ϵ���ж����������ʶ������ǽ���������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{1}{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 0��a��1��b��0 | B�� | 0��a��1��b��0 | C�� | a��1��b��0 | D�� | a��1��b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com