
| A. | 4π | B. | $\frac{32}{3}$π | C. | 16π | D. | 12π |
分析 设△ABC的中心为S,球O的半径为R,△ABC的边长为2a,由已知条件推导出a=$\frac{3}{4}$R,再由三棱锥P-ABC的体积为$\frac{9\sqrt{3}}{4}$,求出R=2,由此能求出球O的表面积.
解答 解:如图,P,A,B,C是球O球面上四点,△ABC是正三角形,
设△ABC的中心为S,球O的半径为R,△ABC的边长为2a,
∵∠APO=∠BPO=∠CPO=30°,
OB=OP=R,
∴OS=$\frac{R}{2}$,BS=$\frac{\sqrt{3}}{2}$R,
∴$\frac{2\sqrt{3}}{3}a$=$\frac{\sqrt{3}}{2}$R,解得a=$\frac{3}{4}$R,2a=$\frac{3}{2}$R,
∵三棱锥P-ABC的体积为 $\frac{9\sqrt{3}}{4}$,∴$\frac{1}{3}$×$\frac{1}{2}$×$\frac{1}{2}$×$\frac{3}{2}$R×$\frac{3}{2}$Rsin60°×$\frac{3}{2}$R=$\frac{9\sqrt{3}}{4}$,
解得R=2,
∴球O的表面积S=4πR2=16π.
故选:C.
点评 本题考查球的表面积的求法,是中档题,解题时确定球O的半径是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
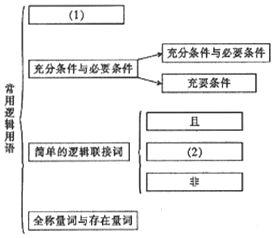
| A. | 命题及其关系、或 | B. | 命题的否定、或 | C. | 命题及其关系、并 | D. | 命题的否定、并 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{e}{3}$,+∞) | B. | [$\frac{e}{3}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | e2<x3x4<(2e-1)2 | C. | 0<(2e-x3)(2e-x4)<1 | D. | 1<x1x2<e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
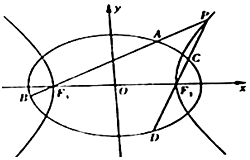 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com