
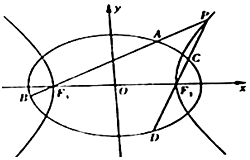
 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.分析 (Ⅰ)由题意知,椭圆离心率为a=$\sqrt{2}$c,及椭圆的定义得到又2a+2c=$4(\sqrt{2}+1)$,解方程组即可求得椭圆的方程,等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程;
(Ⅱ)设点P(x0,y0),根据斜率公式求得k1、k2,把点P(x0,y0)在双曲线上,即可证明结果.
解答 解:(Ⅰ)由题意知,椭圆离心率为e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,则a=$\sqrt{2}$c,
又2a+2c=$4(\sqrt{2}+1)$,
解得:a=2$\sqrt{2}$,c=2,
∴b2=a2-c2=4,
∴椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,
∴椭圆的焦点坐标为(±2,0).
∵双曲线为等轴双曲线,且顶点是该椭圆的焦点,
∴该双曲线的标准方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}=1$;
(Ⅱ)设点P(x0,y0),
则k1=$\frac{{y}_{0}}{{x}_{0}+2}$,k2=$\frac{{y}_{0}}{{x}_{0}-2}$,
∴k1•k2=$\frac{{y}_{0}}{{x}_{0}+2}$×$\frac{{y}_{0}}{{x}_{0}-2}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$,
又点P(x0,y0)在双曲线上,
∴$\frac{{x}_{0}^{2}}{4}-\frac{{y}_{0}^{2}}{4}=1$,即y02=x02-4,
∴k1•k2=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=1.
点评 本题考查椭圆的标准方程及简单几何性质,等轴双曲线的求法,考查了学生综合运用知识解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | $\frac{32}{3}$π | C. | 16π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{4},\frac{4}{3}}]$ | B. | $({0,\frac{3}{4}}]∪[{\frac{4}{3},+∞})$ | C. | $[{\frac{4}{3},+∞})$ | D. | $({0,\frac{3}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sin α<tan α | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限角或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)且k≠0,则sin α=$\frac{4}{5}$ | |
| D. | 若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com