
| A. | 10 | B. | 8 | C. | 6 | D. | 2 |
分析 由f(x)=2x2-4x-1=2(x-1)2-3对任意xi,xj(i,j=1,2,3,…,n),0≤x1<x2<…<xn≤3,都有|f(xi)-f(xj)|≤f(x)max-f(x)min=8,即可得出结论.
解答 解:∵f(x)=2x2-4x-1=2(x-1)2-3对任意xi,xj(i,j=1,2,3,…,n),0≤x1<x2<…<xn≤3,
都有|f(xi)-f(xj)|≤f(x)max-f(x)min=8,
∵|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xn-1)-f(xn)|≤M,
∴|f(x1)-f(xn)|≤M,
∴M≥8,
∴M的最小值是8,
故选B.
点评 本题考查了函数的单调性、函数求最值,考查了推理能力与计算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
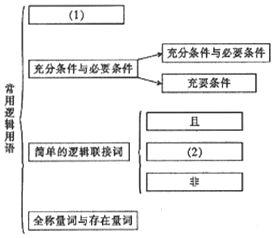
| A. | 命题及其关系、或 | B. | 命题的否定、或 | C. | 命题及其关系、并 | D. | 命题的否定、并 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | e2<x3x4<(2e-1)2 | C. | 0<(2e-x3)(2e-x4)<1 | D. | 1<x1x2<e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {-3,-4} | C. | {-1,-2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
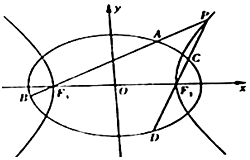 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
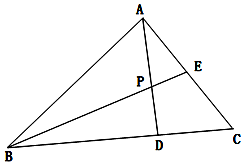 在△ABC中,E为AC中点,D为BC靠近C的三等分点,记$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$.
在△ABC中,E为AC中点,D为BC靠近C的三等分点,记$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com