
分析 (1)分别把n=1和n=n-1代入条件式计算a1和递推公式,得出{an}为等差数列,从而得出通项公式;
(2)求出数列{bn}的通项公式,再由分组求和,分别运用等差数列和等比数列的求和公式,注意公比为1的情况.
解答 (普班、实验班学生做)
解:(1)由Sn=$\frac{1}{4}$an2+$\frac{1}{2}$an+$\frac{1}{4}$①得,当n≥2时,Sn-1=$\frac{1}{4}$an-12+$\frac{1}{2}$an-1+$\frac{1}{4}$②;
由①-②化简得::(an+an-1)(an-an-1-2)=0,
又∵数列{an}各项为正数,
∴当n≥2时,an-an-1=2,故数列{an}成等差数列,公差为2,又S1=$\frac{1}{4}$a12+$\frac{1}{2}$a1+$\frac{1}{4}$,
解得a1=1,an=1+2(n-1)=2n-1;
∵数列{an+bn}是首项为1,公比为q的等比数列,
∴an+bn=qn-1,
∴bn=-2n+1+qn-1,
∴Sn=-n2+(1+q+q2+…+qn-1)
当q=1时,Sn=-n2+n;
当q≠1时,Sn=-n2+$\frac{1-{q}^{n}}{1-q}$
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查分类讨论的思想方法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -9 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
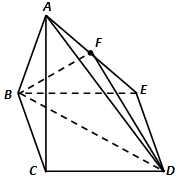 如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.
如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sin α<tan α | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限角或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)且k≠0,则sin α=$\frac{4}{5}$ | |
| D. | 若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 2-2ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2018}+1$ | B. | $\sqrt{2018}-1$ | C. | $\sqrt{2017}-1$ | D. | $\sqrt{2017}+1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com