
分析 根据特殊元素优先安排,相邻问题用捆绑,不相邻用插空法,即可求解.
解答 解:(1)男生必须排在一起把4名男生捆绑在一起看做一个复合元素,再和3位女生全排,故有A44A44=576种;
(2)甲、乙中间必须有2人,从5人选2人和甲乙捆绑在一起,再和另外3人全排列,故有A52A22A44=960种;
(3)三女生互不相邻,先排男生形成了5个空中,插入3名女生,故有A44A53=1440种;
(4)甲、乙必须在两端;A22A55=240种
(5)甲、乙两位同学不得排两端,先从5人选2排在两端,剩下的全排,故有A52A55=2400种;
(6)把甲乙两位女生捆绑在一起和另一位女生插入到男生形成了5个空中,故有A22A44A52=690种.
点评 本题考查排列的应用,相邻问题一般看作一个整体处理,不相邻,用插空法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
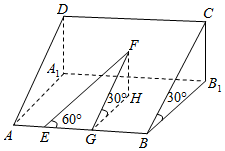 如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?
如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com