
| A. | 2 | B. | $\frac{4\sqrt{5}}{5}$ | C. | 3 | D. | $\sqrt{5}$ |
分析 由题意画出图形,把问题转化为在抛物线y2=4x上找一点P,使得P到F的距离和到直线l1:2x-y+2=0的距离和最小,再用点到直线的距离公式求解.
解答 解:由抛物线y2=4x,得焦点坐标为F(1,0),准线方程为l2:x=-1,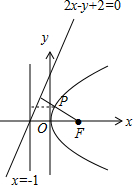
由抛物线定义知,P到直线l2的距离等于P到抛物线焦点F得距离.
故问题化为在抛物线y2=4x上找一点P,使得P到F的距离和到直线l1:2x-y+2=0的距离和最小.
最小值为F到l1:2x-y+2=0的距离,等于$\frac{|2-0+2|}{\sqrt{4+1}}=\frac{4\sqrt{5}}{5}$.
故选:B.
点评 本题考查抛物线的简单性质,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
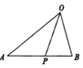 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 逆时针方向匀速前跑 | B. | 顺时针方向匀速前跑 | ||
| C. | 顺时针方向匀速后退 | D. | 静止不动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com