
已知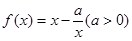 ,
,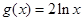 ,
,
(1)若对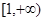 内的一切实数
内的一切实数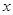 ,不等式
,不等式 恒成立,求实数
恒成立,求实数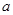 的取值范围;
的取值范围;
(2)当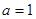 时,求最大的正整数
时,求最大的正整数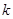 ,使得对
,使得对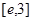 (
(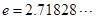 是自然对数的底数)内的任意
是自然对数的底数)内的任意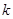 个实数
个实数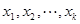 都有
都有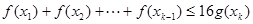 成立;
成立;
(3)求证:
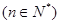 .
.
(1)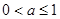 . (2)
. (2)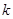 的最大值为
的最大值为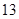 .
.
(3)证明(法一):先得到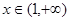 时,
时,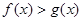 ,即
,即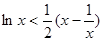 .
.
令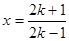 ,得
,得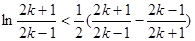 ,
,
化简得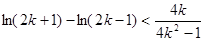 ,
, 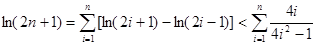 .
.
(法二)数学归纳法:
解析试题分析:(1)由 得
得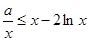 ,
,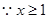 ,
,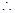 要使不等式
要使不等式 恒成立,必须
恒成立,必须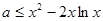 恒成立.
恒成立.
设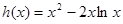 ,
, ,
,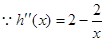 ,
,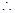 当
当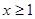 时,
时,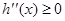 ,则
,则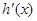 是增函数,
是增函数,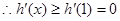 ,
,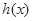 是增函数,
是增函数,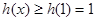 ,
,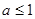 .
.
因此,实数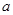 的取值范围是
的取值范围是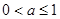 . 5分
. 5分
(2)当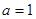 时,
时,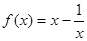 ,
,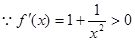 ,
,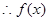 在
在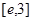 上是增函数,
上是增函数,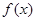 在
在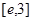 上的最大值为
上的最大值为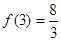 .
.
要对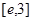 内的任意
内的任意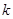 个实数
个实数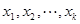 都有
都有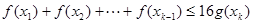
成立,必须使得不等式左边的最大值小于或等于右边的最小值,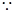 当
当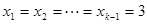 时不等式左边取得最大值,
时不等式左边取得最大值,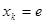 时不等式右边取得最小值.
时不等式右边取得最小值.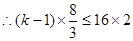 ,解得
,解得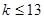 .
.
因此,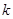 的最大值为
的最大值为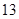 . 9分
. 9分
(3)证明(法一):当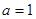 时,根据(1)的推导有,
时,根据(1)的推导有,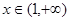 时,
时,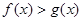 ,
,
即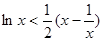 . 10分
. 10分
令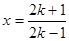 ,得
,得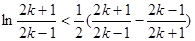 ,
,
化简得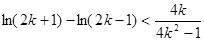 , 13分
, 13分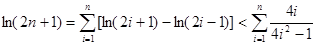 . 14分
. 14分
(法二)数学归纳法:当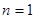 时,左边=
时,左边=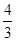 ,右边=
,右边=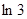 ,
,
根据(1)的推导有,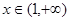 时,
时,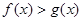 ,即
,即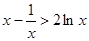 .
.
令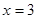 ,得
,得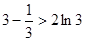 ,即
,即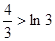 . 因此,
. 因此,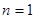 时不等式成立. 10分
时不等式成立. 10分
(另解: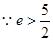 ,
,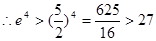 ,
,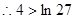 ,即
,即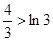 .)
.)
假设当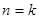 时不等式成立,即
时不等式成立,即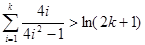 ,
,
则当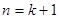 时,
时,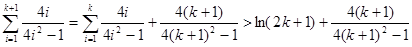 ,
,
要证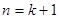 时命题成立,即证
时命题成立,即证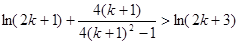


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com