
分析 设直线AB的方程为:y=k(x-$\frac{p}{2}$)(k≠0).由于AB⊥CD,可得直线CD的方程为y=-$\frac{1}{k}$(x-$\frac{p}{2}$),分别与抛物线的方程联立可得根与系数的关系,再利用向量的坐标运算和数量积运算,即可证得$\frac{1}{\overrightarrow{FA•}\overrightarrow{FB}}+$$\frac{1}{\overrightarrow{FC}•\overrightarrow{FD}}$为定值.
解答 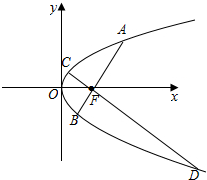 证明:如图所示,由抛物线y2=2px,可得焦点F($\frac{p}{2},0$).
证明:如图所示,由抛物线y2=2px,可得焦点F($\frac{p}{2},0$).
设直线AB的方程为:y=k(x-$\frac{p}{2}$)(k≠0),
∵AB⊥CD,可得直线CD的方程为y=-$\frac{1}{k}$(x-$\frac{p}{2}$),
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).
联立$\left\{\begin{array}{l}{y=k(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,化为4k2x2-(4k2p+8p)x+k2p2=0,
得x1+x2=$\frac{{k}^{2}p+2p}{{k}^{2}}$,x1x2=$\frac{{p}^{2}}{4}$.
同理可得x3+x4=p+2k2p,x3x4=$\frac{{p}^{2}}{4}$.
∴$\overrightarrow{FA}•\overrightarrow{FB}$=(x1$-\frac{p}{2}$,y1)•(x2-$\frac{p}{2}$,y2)=x1x2-$\frac{p}{2}({x}_{1}+{x}_{2})$+$\frac{{p}^{2}}{4}$+y1•y2
=x1x2-$\frac{p}{2}({x}_{1}+{x}_{2})$+$\frac{{p}^{2}}{4}$+${k}^{2}{x}_{1}{x}_{2}-\frac{{k}^{2}p}{2}({x}_{1}+{x}_{2})+\frac{{k}^{2}{p}^{2}}{4}$
=$({k}^{2}+1){x}_{1}{x}_{2}-(\frac{{k}^{2}p}{2}+\frac{p}{2})({x}_{1}+{x}_{2})+\frac{{p}^{2}}{4}({k}^{2}+1)$
=$({k}^{2}+1)[\frac{{p}^{2}}{4}-\frac{p}{2}\frac{{k}^{2}p+2p}{{k}^{2}}+\frac{{p}^{2}}{4}]$=$-\frac{{p}^{2}({k}^{2}+1)}{{k}^{2}}$;
同理可得$\overrightarrow{FC}•\overrightarrow{FD}$=-p2(k2+1).
∴$\frac{1}{\overrightarrow{FA•}\overrightarrow{FB}}+$$\frac{1}{\overrightarrow{FC}•\overrightarrow{FD}}$=$-\frac{{k}^{2}}{{p}^{2}({k}^{2}+1)}-\frac{1}{{p}^{2}({k}^{2}+1)}=-\frac{{k}^{2}+1}{{p}^{2}({k}^{2}+1)}$=$-\frac{1}{{p}^{2}}$,为定值.
点评 本题考查直线与抛物线位置关系的应用,联立直线方程与抛物线方程,化为关于x的一元二次方程,利用根与系数的关系求解是解题的关键,考查向量的坐标运算和数量积运算,考查了推理论证能力和计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
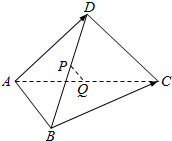 如图,P,Q分别为四边形ABCD的对角线BD,AC的中点,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{PQ}$.
如图,P,Q分别为四边形ABCD的对角线BD,AC的中点,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com