
分析 (1)利用等比数列的通项公式与性质、等差数列的通项公式与求和公式即可得出.
(2)分类讨论,利用“裂项求和”方法即可得出.
解答 解:(1)∵3$\sqrt{5}$是-a2与a9的等比中项,∴$(3\sqrt{5})^{2}$=-a2•a9,又S10=-20.
∴-(a1+d)(a1+8d)=45,10a1+$\frac{10×9}{2}$d=-20,
联立解得a1=-11,d=2.
∴an=-11+2(n-1)=2n-13.
(2)1≤n≤5时,bn=$\frac{1}{{a}_{n}|{a}_{n+1}|}$=$\frac{1}{(2n-13)(11-2n)}$=-$\frac{1}{2}(\frac{1}{2n-13}-\frac{1}{2n-11})$.
n≥6,bn=$\frac{1}{{a}_{n}|{a}_{n+1}|}$=$\frac{1}{(2n-13)(2n-11)}$=$\frac{1}{2}(\frac{1}{2n-13}-\frac{1}{2n-11})$,
∴n≥6时,数列{bn}的前n项和Tn=-$\frac{1}{2}$$(-\frac{1}{11}+1)$+$\frac{1}{2}$$(-1-\frac{1}{2n-11})$
=$-\frac{21}{22}$-$\frac{1}{4n-22}$.
点评 本题考查了等差数列的通项公式与求和公式、分类讨论、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
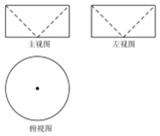 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
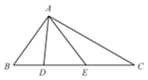 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{21}{2}$ | D. | $\frac{33}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com