
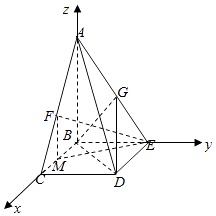
【题目】如图所示,在四棱锥A﹣BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE= ![]() .
.
(Ⅰ)证明:EF⊥BD;
(Ⅱ)在线段AE上是否存在一点G,使得二面角D﹣BG﹣E的大小为 ![]() ?若存在,求
?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】证明:(Ⅰ)取BC的中点M,连接MF,ME,
∵AB⊥平面BCDE,MF∥AB,
∴MF⊥平面BCDE,又BD平面BCDE,∴MF⊥BD.
在Rt△MBE与Rt△BED中,
∵ ![]() =
= ![]() =
= ![]() ,∴Rt△MBE∽Rt△BED.
,∴Rt△MBE∽Rt△BED.
∴∠BME=∠EBD,而∠BME+∠BEM=90°,
于是∠BEM+∠EBD=90°,∴ME⊥BD,
又∵MF∩ME=M,∴BD⊥平面MEF,
又∵EF平面MEF,∴EF⊥BD.
解:(Ⅱ)∵AB⊥平面BCDE,四边形BCDE为矩形,
∴以B为原点,分别以 ![]() 、
、 ![]() 、
、 ![]() 的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
设AG=λAE,依题意可得B(0,0,0),C(2,0,0),
D(2, ![]() ,0),A(0,0,2),E(0,
,0),A(0,0,2),E(0, ![]() ,0),F(1,0,1),
,0),F(1,0,1),
∴ ![]() =
= ![]() +
+ ![]() =
= ![]() +λ
+λ ![]() =(0,
=(0, ![]() λ,2﹣2λ),
λ,2﹣2λ), ![]() =(2,
=(2, ![]() ,0),
,0),
设平面BGD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 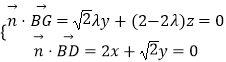 ,取x=1,则
,取x=1,则 ![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() ),
),
平面BGE的法向量为 ![]() =(1,0,0),
=(1,0,0),
∵二面角D﹣BG﹣E的大小为 ![]() ,
,
∴|cos< ![]() ,
, >|=
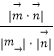 =
= ![]() =
= ![]() ,解得λ=
,解得λ= ![]() .
.
∴存在一点G,且 ![]() =
= ![]() 时,二面角D﹣BG﹣E的大小为
时,二面角D﹣BG﹣E的大小为 ![]() .
.
【解析】(Ⅰ)求两条异面直线互相垂直,可以求得一直线垂直于另一直线所在平面,进而证明两条异面直线互相垂直;(Ⅱ)根据题意建立合适的空间直角坐标系,令二面角D﹣BG﹣E的大小为![]() ,求得此时点G的位置,即可解题 .
,求得此时点G的位置,即可解题 .
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知过点(0,1)的直线与圆x2+y2=4相交于A、B两点,若 ![]() ,则点P的轨迹方程是( )
,则点P的轨迹方程是( )
A.![]()
B.x2+(y﹣1)2=1
C.![]()
D.x2+(y﹣1)2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是抛物线M:y2=2px(p>0)与圆C:x2+(y﹣4)2=a2在第一象限的公共点,且点A到抛物线M焦点F的距离为a,若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,O为坐标原点,则直线OA被圆C所截得的弦长为( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“a=﹣1”是“直线ax+3y+2=0与直线x+(a﹣2)y+1=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
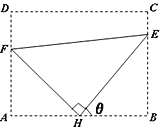
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
, ![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点, ![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米, ![]() 米,记
米,记![]() .
.
(1)试将污水净化管道的总长度![]() (即
(即![]() 的周长)表示为
的周长)表示为![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)问![]() 当取何值时,污水净化效果最好?并求出此时管道的总长度.
当取何值时,污水净化效果最好?并求出此时管道的总长度.
(提示: ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正三棱锥A﹣BCD(底面是正三角形,顶点在底面的射影为底面中心)的所有顶点都在球O的球面上,BC=2,E,F分别是AB,BC的中点,EF⊥DE,则球O的表面积为( )
A.![]()
B.6π
C.8π
D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(II)设![]() 为圆
为圆![]() 上的两个动点,
上的两个动点, ![]() ,若直线
,若直线![]() 和
和![]() 的斜率之积为定值2,试探求
的斜率之积为定值2,试探求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com