
设函数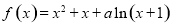 ,其中
,其中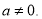
(1)若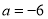 ,求
,求 在
在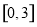 上的最值;
上的最值;
(2)若 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(3)当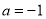 时,令
时,令 ,试证:
,试证: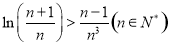 恒成立.
恒成立.
(1)参考解析,(2)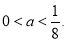 (3)参考解析
(3)参考解析
【解析】
试题分析:(1)当 时,对函数
时,对函数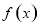 求导,在定义域内根据导函数的正负性可得到函数的单调性,即可求得函数的最值.
求导,在定义域内根据导函数的正负性可得到函数的单调性,即可求得函数的最值.
(2)由函数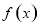 在定义域内既有极大值又有极小值,即导函数的值为零时的根在
在定义域内既有极大值又有极小值,即导函数的值为零时的根在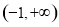 上有两个不等的实数解.再根据区间根的运算即可得到结论.
上有两个不等的实数解.再根据区间根的运算即可得到结论.
(3)当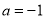 时,对
时,对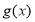 求导即可得到, 即
求导即可得到, 即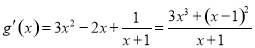 ,所以当
,所以当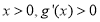 恒成立,由题意要证
恒成立,由题意要证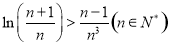 ,其中的变量为正数,所以当
,其中的变量为正数,所以当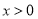 时,函数
时,函数 是单调递增的.再通过令
是单调递增的.再通过令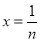 .
.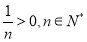 ,以及
,以及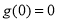 即可得到结论.
即可得到结论.
试题解析:(1)由题意知,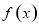 的定义域为
的定义域为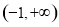 ,
,
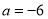 时,由
时,由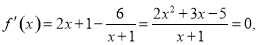
得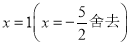 2分
2分
当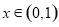 时,
时,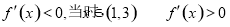 ,
,
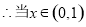 ,
,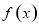 单调递减,当
单调递减,当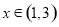 时,
时,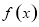 单调递增.
单调递增.
所以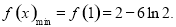
又因为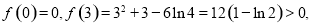
所以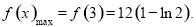
所以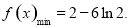 ,
,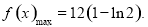
(2)依题意,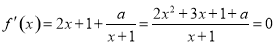 在
在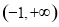 上有两个不等实根,即
上有两个不等实根,即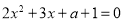 在
在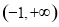 上有两个不等实根, 6分
上有两个不等实根, 6分
设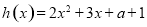 ,则
,则 ,解得
,解得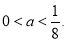 8分
8分
(3)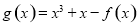 =
=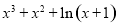 ,
,
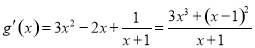
显然,当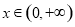 时,
时,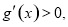 所以
所以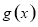 在
在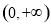 上单调递增,
上单调递增,
所以,当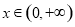 时,
时,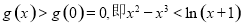 恒成立. 10分
恒成立. 10分
令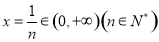 ,则有
,则有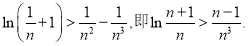 12分
12分
考点:1.利用导数求函数的最值.2.函数的极值.3.函数与不等式的关系.4.构建函数的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届河南省原名校高三上学期第一次摸底考试数学文科数学试卷(解析版) 题型:选择题
己知 ,则“a=±1”是“
,则“a=±1”是“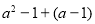 i为纯虚数”的( )
i为纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届河北省邯郸市高三上学期摸底考试文科数学试卷(解析版) 题型:选择题
设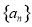 是公差为正数的等差数列,若
是公差为正数的等差数列,若 ,
,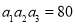 ,则
,则 ( )
( )
A、75 B、90 C、105 D、120
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知x>0,由不等式x+ ≥2
≥2 =2,x+
=2,x+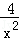 =
= ≥3
≥3 =3,…,可以推出结论:x+
=3,…,可以推出结论:x+ ≥n+1(n∈N*),则a=( ).
≥n+1(n∈N*),则a=( ).
A.2n B.3n C.n2 D.nn
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设随机变量X服从正态分布N(3,4),若P(X<2a+3)=P(X>a﹣2),则a的值为( ).
A.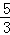 B.3 C.5 D.
B.3 C.5 D.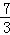
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
直线l: 与曲线
与曲线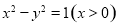 相交于A、B两点,则直线l倾斜角的取值范围是( )
相交于A、B两点,则直线l倾斜角的取值范围是( )
A. B.
B. C.
C.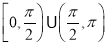 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省红色六校高三第一次联考文科数学试卷(解析版) 题型:解答题
已知数列 的前
的前 项和为
项和为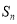 ,且
,且
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设
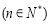 ,
, ,求使
,求使 成立的最小的正整数
成立的最小的正整数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com