Question

15．海水受日月的引力，在一定的时候发生涨落的现象叫潮．一般地，早潮叫潮，晚潮叫汐．在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋．下面是某港口在某季节每天时间与水深（单位：米）的关系表：

时刻	0：00	3：00	6：00	9：00	12：00	15：00	18：00	21：00	24：00
水深	10.0	13.0	9.9	7.0	10.0	13.0	10.1	7.0	10.0

（1）请用一个函数来近似描述这个港口的水深y与时间t的函数关系；
（2）一般情况下，船舶航行时，船底离海底的距离为5米或5米以上认为是安全的（船舶停靠时，船底只要不碰海底即可）．某船吃水深度（船底离地面的距离）为6.5米．
Ⅰ）如果该船是旅游船，1：00进港希望在同一天内安全出港，它至多能在港内停留多长时间（忽略进出港所需时间）？
Ⅱ）如果该船是货船，在2：00开始卸货，吃水深度以每小时0.5米的速度减少，由于台风等天气原因该船必须在10：00之前离开该港口，为了使卸下的货物尽可能多而且能安全驶离该港口，那么该船在什么整点时刻必须停止卸货（忽略出港所需时间）？

Answer 1

分析 （1）设出函数解析式，据最大值与最小值的差的一半为A；最大值与最小值和的一半为h；通过周期求出ω，得到函数解析式．
（2）Ⅰ）据题意列出不等式，利用三角函数的周期性及单调性解三角不等式求出t的范围．
Ⅱ）设f（x）=3sin$\frac{π}{6}$x+10，x∈[2，10]，g（x）=11.5-0.5（x-2）（x≥2）对它们进行比较从而得到答案．

解答 （1）以时间为横坐标，水深为纵坐标，在直角坐标系中画出散点图．如图．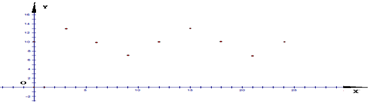
根据图象，可考虑用函数y=Asin（ωx+φ）+h刻画水深与时间之间的对应关系．
从数据和图象可以得出A=3，h=10，T=12，φ=0，
由T=$\frac{2π}{ω}$=12，得ω=$\frac{π}{6}$，所以这个港口水深与时间的关系可用y=3sin$\frac{π}{6}$t+10近似描述…（4分）
（2）Ⅰ）由题意，y≥11.5就可以进出港，令sin$\frac{π}{6}$t=$\frac{1}{2}$，如图，在区间[0，12]内，
函数y=3sin$\frac{π}{6}$t+10 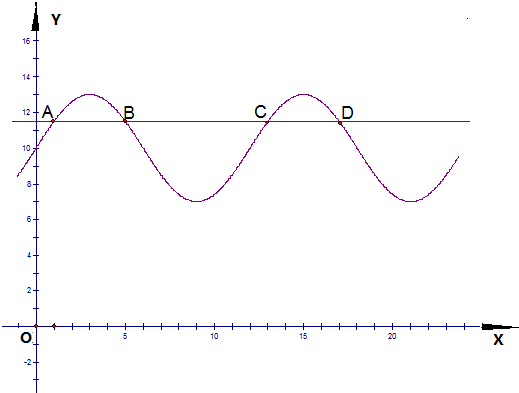与直线y=11.5有两个交点，由sin$\frac{π}{6}$t=$\frac{π}{6}$或$\frac{5}{6}π$，
得x_A=1，x_B=5，由周期性得x_C=13，x_D=17，
由于该船从1：00进港，可以17：00离港，所以在同一天安全出港，在港内停留的最多时间是16小时…（8分）
Ⅱ）设在时刻x货船航行的安全水深为y，那么y=11.5-0.5（x-2）（x≥2）．
设f（x）=3sin$\frac{π}{6}$x+10，x∈[2，10]，
g（x）=11.5-0.5（x-2）（x≥2）
由f（6）=10＞g（6）=9.5且f（7）=8.5＜g（7）=9知，
为了安全，货船最好在整点时刻6点之前停止卸货…（13分）

点评 本题考查通过待定系数法求函数解析式、利用三角函数的单调性及周期性解三角不等式．