
| A. | ①③ | B. | ③④ | C. | ①②③ | D. | ①③④ |
分析 对于①,根据射影的定义即可判断;
对于②,根据三垂线定理的逆定理可知,O是△BCD的垂心,
对于③在正方体中,找出满足题意的四面体,即可得到直角三角形的个数,
对于④作出正四面体的图形,球的球心位置,说明OE是内切球的半径,利用直角三角形,逐步求出内切球的表面积.
解答 解:对于①,设点A在平面BCD内的射影是O,因为AB=AC=AD,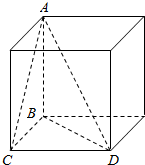 所以OB=OC=OD,
所以OB=OC=OD,
则点A在底面BCD内的射影是△BCD的外心,故①正确;
对于②设点A在平面BCD内的射影是O,则OB是AB在平面BCD内的射影,因为AB⊥CD,根据三垂线定理的逆定理可知:CD⊥OB 同理可证BD⊥OC,所以O是△BCD的垂心,故②不正确;
对于③:如图:直接三角形的直角顶点已经标出,直角三角形的个数是4.故③正确
对于④,如图O为正四面体ABCD的内切球的球心,正四面体的棱长为:1;
所以OE为内切球的半径,BF=AF=$\frac{\sqrt{3}}{2}$,BE=$\frac{\sqrt{3}}{3}$,
所以AE=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,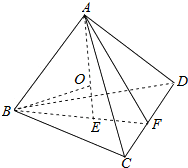
因为BO2-OE2=BE2,
所以($\frac{\sqrt{6}}{3}$-OE)2-OE2=($\frac{\sqrt{3}}{3}$)2,
所以OE=$\frac{\sqrt{6}}{12}$,
所以球的表面积为:4π•OE2=$\frac{π}{6}$,故④正确.
故选D.
点评 本题考查命题的真假判断与应用,综合考查了线面、面面垂直的判断与性质,考查了学生的空间想象能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 128 | C. | 192 | D. | 384 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒小于零 | B. | 恒等于零 | ||
| C. | 恒大于零 | D. | 可能大于零,也可能小于零 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ③④ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $16({π-\sqrt{3}})$ | B. | $16({π-\sqrt{2}})$ | C. | $8({2π-3\sqrt{2}})$ | D. | $8({2π-\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50π | B. | 100π | C. | 200π | D. | $\frac{{125\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
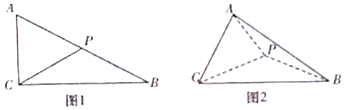 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com