
分析 (1)求出原函数的导函数,由f(x)在x=0处取得极值,且x-ey=0是曲线y=f(x)的切线,可得b=1,且$\left\{{\begin{array}{l}{\frac{1}{e}{x_0}=\frac{ax_0^2}{{{e^{x_0}}}}}\\{\frac{1}{e}=\frac{{-ax_0^2+2a{x_0}}}{{{e^{x_0}}}}}\end{array}}\right.$,由此可得a值;
(2)记函数$F(x)=f(x)-(x-\frac{1}{x})=\frac{x^2}{e^x}-x+\frac{1}{x},x>0$,求其导函数,可得当x≥2时,F'(x)<0恒成立,当0<x<2时,F'(x)<0在(0,+∞)上恒成立,故F(x)在(0,+∞)上单调递减.由函数的零点存在性定理及其单调性知存在唯一的x0∈(1,2),使F(x0)=0,有$g(x)=min\left\{{f(x),x-\frac{1}{x}}\right\}=\left\{{\begin{array}{l}{x-\frac{1}{x},0<x≤{x_0}}\\{\frac{x^2}{e^x},x>{x_0}}\end{array}}\right.$,得到$h(x)=g(x)-c{x^2}=\left\{{\begin{array}{l}{x-\frac{1}{x}-c{x^2},0<x≤{x_0}}\\{\frac{x^2}{e^x}-c{x^2},x>{x_0}}\end{array}}\right.$,分离参数c后利用导数求得答案.
解答 解:(1)$f'(x)=\frac{{(2ax+b){e^x}-(a{x^2}+bx){e^x}}}{{{{({e^x})}^2}}}=\frac{{-a{x^2}+(2a-b)x+b}}{e^x}$,
∵f(x)在x=0处取得极值,∴f'(0)=0,即b=0,
此时$f(x)=\frac{{a{x^2}}}{e^x},f'(x)=\frac{{-a{x^2}+2ax}}{e^x}$,
设直线x-ey=0与曲线y=f(x)切于点P(x0,y0),由题意得$\left\{{\begin{array}{l}{\frac{1}{e}{x_0}=\frac{ax_0^2}{{{e^{x_0}}}}}\\{\frac{1}{e}=\frac{{-ax_0^2+2a{x_0}}}{{{e^{x_0}}}}}\end{array}}\right.$,解之得a=1;
(2)记函数$F(x)=f(x)-(x-\frac{1}{x})=\frac{x^2}{e^x}-x+\frac{1}{x},x>0$$F'(x)=\frac{x(2-x)}{e^x}-1-\frac{1}{x^2},x>0$,
当x≥2时,F'(x)<0恒成立,
当0<x<2时,$x(2-x)≤{[\frac{x+(2-x)}{2}]^2}=1$,
从而$F'(x)=\frac{x(2-x)}{e^x}-1-\frac{1}{x^2}≤\frac{1}{e^x}-1-\frac{1}{x^2}<1-1-\frac{1}{x^2}=-\frac{1}{x^2}<0$
∴F'(x)<0在(0,+∞)上恒成立,故F(x)在(0,+∞)上单调递减.
又$F(1)=\frac{1}{e}>0,F(2)=\frac{4}{e^2}-\frac{3}{2}<0$,∴F(1)•F(2)<0,
又曲线y=F(x)在[1,2]上连续不间断,
∴由函数的零点存在性定理及其单调性知存在唯一的x0∈(1,2),使F(x0)=0,
∴x∈(0,x0),F(x)>0;x∈(x0,+∞),F(x)<0,
故$g(x)=min\left\{{f(x),x-\frac{1}{x}}\right\}=\left\{{\begin{array}{l}{x-\frac{1}{x},0<x≤{x_0}}\\{\frac{x^2}{e^x},x>{x_0}}\end{array}}\right.$,
从而$h(x)=g(x)-c{x^2}=\left\{{\begin{array}{l}{x-\frac{1}{x}-c{x^2},0<x≤{x_0}}\\{\frac{x^2}{e^x}-c{x^2},x>{x_0}}\end{array}}\right.$,
∴$h'(x)=\left\{{\begin{array}{l}{1+\frac{1}{x^2}-2cx,0<x≤{x_0}}\\{\frac{x(2-x)}{e^x}-2cx,x>{x_0}}\end{array}}\right.$.
由函数h(x)=g(x)-cx2为增函数,且曲线y=h(x)在(0,+∞)上连续不断,
知h'(x)≥0在(0,x0),(x0,+∞)上恒成立.
①当x>x0时,$\frac{x(2-x)}{e^x}-2cx≥0$在(x0,+∞)上恒成立,
即$2c≤\frac{2-x}{e^x}$在(x0,+∞)上恒成立,记$u(x)=\frac{2-x}{e^x}$,则$u'(x)=\frac{x-3}{e^x}$,
从而u(x)在(x0,3)单调递减,在(3,+∞)单调递增,∴$u{(x)_{min}}=u(3)=-\frac{1}{e^3}$.
故$2c≤\frac{2-x}{e^x}$在(x0,+∞)上恒成立,只需$2c≤u(x){\;}_{min}=-\frac{1}{e^3}$,∴$c≤-\frac{1}{{2{e^3}}}$.
②当0<x<x0时,$h'(x)=1+\frac{1}{x^2}-2cx$,
当c≤0时,h'(x)>0在(0,x0)上恒成立,
综上所述,实数c的取值范围为:$c≤-\frac{1}{{2{e^3}}}$.
点评 本题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等,是压轴题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{2}$ | B. | 4 | C. | $\sqrt{34}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
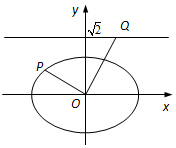 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
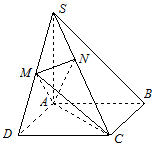 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com