
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 先根据二倍角公式降幂,再由诱导公式以及积化和差、和差化积公式进行化简,即可得到答案.
解答 解:sin240°+sin220°+sin40°•sin20°
=$\frac{1}{2}$(1-cos80°)+$\frac{1}{2}$(1-cos40°)+sin40°cos70°
=1-$\frac{1}{2}$(cos80°+cos40°)+$\frac{1}{2}$[sin110°+sin(-30°)]
=1-cos60°cos20°+$\frac{1}{2}$cos20°-$\frac{1}{4}$
=$\frac{3}{4}$.
故选:A.
点评 本题主要考查三角恒等变换与诱导公式的灵活应用问题式,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y+1=0 | B. | x+y+1=0 | C. | x+y-7=0 | D. | x-y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 24 | C. | 22 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
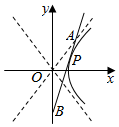 已知双曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),离心率e=$\frac{\sqrt{13}}{2}$.
已知双曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),离心率e=$\frac{\sqrt{13}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com