
【题目】已知椭圆C![]() 的一焦点与
的一焦点与![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆C上.直线l过点(1,1),且与椭圆C交于A,B两点.
在椭圆C上.直线l过点(1,1),且与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)点M满足![]() ,点O为坐标原点,延长线段OM与椭圆C交于点P,四边形OAPB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与椭圆C交于点P,四边形OAPB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
【答案】(1)![]() y2=1;(2)能,x=1或3x﹣8y+5=0.
y2=1;(2)能,x=1或3x﹣8y+5=0.
【解析】
(1)求出抛物线焦点坐标,即为椭圆一焦点,可得![]() 的一方程,由已知点在椭圆上又得一个
的一方程,由已知点在椭圆上又得一个![]() 的方程,联立后可解得
的方程,联立后可解得![]() ,得椭圆方程;
,得椭圆方程;
(2)假设存在四边形OAPB为平行四边形,需要分类讨论,当直线![]() 的斜率不存在时,即x=1,可求得
的斜率不存在时,即x=1,可求得![]() 点坐标,得证,当直线
点坐标,得证,当直线![]() 的斜率存在时,设l的方程为:y=kx+m,显然k≠0,m≠0,设
的斜率存在时,设l的方程为:y=kx+m,显然k≠0,m≠0,设![]() ,
,![]() , M(x0,y0),由直线方程与椭圆方程联立,应用韦达定理求得
, M(x0,y0),由直线方程与椭圆方程联立,应用韦达定理求得![]() 点坐标,再由平行四边形得
点坐标,再由平行四边形得![]() 点坐标,利用直线
点坐标,利用直线![]() 过点
过点![]() 及
及![]() 在椭圆上,可求得
在椭圆上,可求得![]() (交待此时直线与椭圆相交),得直线方程.
(交待此时直线与椭圆相交),得直线方程.
(1)![]() 的焦点为:(
的焦点为:(![]() ,0),由题意得c
,0),由题意得c![]() ,点
,点![]() 在椭圆C上,
在椭圆C上,
∴![]() 1,又a2=b2+c2∴a2=4,b2=1,
1,又a2=b2+c2∴a2=4,b2=1,
所以椭圆C的方程为:![]() y2=1;
y2=1;
(2)假设存在四边形OAPB为平行四边形,当直线的斜率不存在时,即x=1,
则A(1,![]() ),B(1,
),B(1,![]() ),
),
则中点M的坐标(1,0),
所以P的坐标(2,0),这时![]() (1,
(1,![]() ),
),
![]() (1,
(1,![]() ),∴
),∴![]() ,
,
所以符合题意,这时直线l的方程:x=1,
当直线的斜率存在时,设l的方程为:y=kx+m,显然k≠0,m≠0,
设![]() ,
,![]() , M(x0,y0),
, M(x0,y0),
将直线与椭圆联立整理得:(4k2+1)x2+8kmx+4m2﹣4=0,△>0,
![]()
![]() ,
,![]()
![]() ,
,
所以M(![]() ,
,![]() ),
),
四边形OAPB为平行四边形时,当且仅当线段AB与线段OP互相平分,即:xP=2x0,yP=2y0,
则 ,
,
又直线l过(1,1),
所以 m=1﹣k,两式联立得:k![]() ,m
,m![]() ,满足△>0,符合条件,
,满足△>0,符合条件,
所以这时直线l的方程:y![]() x
x![]() ,即:3x﹣8y+5=0
,即:3x﹣8y+5=0
综上所述直线l的方程:x=1或3x﹣8y+5=0.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为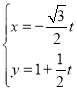 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了调查学生的学习情况,由每班随机抽取![]() 名学生进行调查,若一班有
名学生进行调查,若一班有![]() 名学生,将每一学生编号从
名学生,将每一学生编号从![]() 到
到![]() ,请从随机数表的第
,请从随机数表的第![]() 行第
行第![]() 、
、![]() 列(下表为随机数表的前
列(下表为随机数表的前![]() 行)开始,依次向右,直到取足样本,则第五个编号为_________.
行)开始,依次向右,直到取足样本,则第五个编号为_________.
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+3|+|2x﹣1|.
(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)<|m﹣1|的解集非空,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,则________.(写出所有正确结论的编号)
,则________.(写出所有正确结论的编号)
①四面体![]() 每个面的面积相等
每个面的面积相等
②四面体![]() 每组对棱相互垂直
每组对棱相互垂直
③连接四面体![]() 每组对棱中点的线段相互垂直平分
每组对棱中点的线段相互垂直平分
④从四面体![]() 每个顶点出发的三条棱的长都可以作为一个三角形的三边长
每个顶点出发的三条棱的长都可以作为一个三角形的三边长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(3m2﹣2m)x![]() 在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
(1)求实数m的值;
(2)当x∈[1,9]时,记f(x),g(x)的值域分别为集合A,B,设命题p:x∈A,命题q:x∈B,若命题p是命题q的充分不必要条件,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com