
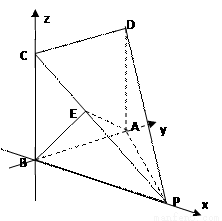
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=60°.
(1)求证:平面PBC⊥面PDC
(2)设E为PC上一点,若二面角B-EA-P的余弦值为- ,求三棱锥E-PAB的体积.
,求三棱锥E-PAB的体积.

(1)见解析
(2) 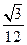
【解析】(1)∵AB=1,PA=2,∠PAB=60°,∴在△PAB中,由余弦定理得
PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×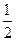 =3
=3
∴PA2=PB2+AB2,即AB⊥PB
∵DA⊥面ABP,CB∥DA
∴CB⊥面ABP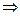 CB⊥AB ,∴AB⊥面PBC
CB⊥AB ,∴AB⊥面PBC
又DC∥AB,∴DC∥面PBC
∵DC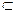 面PDC,∴平面PBC⊥面PDC
面PDC,∴平面PBC⊥面PDC
(2)如图建立空间直角坐标系
则A(0,1,0),P(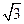 ,0,0),C(0,0,1)
,0,0),C(0,0,1)
设E(x,y,z),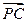 =
= 
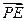 (0<
(0<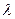 <1)
<1)
则(-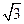 ,0,1)=
,0,1)= (x-
(x-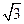 ,y,z)
,y,z)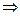 x=
x=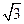 (1-
(1-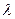 ),y=0,z=
),y=0,z=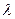
设面ABE的法向量为n=(a,b,c), 则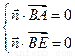
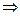
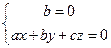
令c=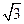
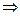

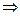 n=(
n=(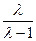 ,0,
,0,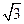 )
)
同理可求平面PAE的法向量为m=(1,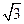 ,
,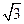 )
)
∵cos<n,m>=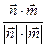 =
=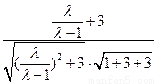 =
=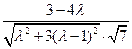 =
=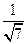
∴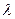 =
=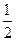 或
或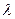 =1(舍去)
=1(舍去)
∴E(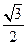 ,0,
,0,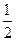 )为PC的中点,其竖坐标即为点E到底面PAB的距离
)为PC的中点,其竖坐标即为点E到底面PAB的距离
∴VE-PAB=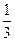 ×
×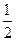 ×1×
×1×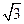 ×
×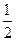 =
=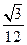


科目:高中数学 来源:2015届上海市高二下学期期中数学试卷(解析版) 题型:填空题
将三个1、三个2、三个3填入3×3的方格中,要求每行、每列都没有重复数字,则不同的填写方法共有 种。
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测二(解析版) 题型:选择题
过抛物线x2=2py(p>0)焦点的直线与抛物线交于不同的两点A、B,则抛物线上A、B两点处的切线斜率之积是( )
A.P2 B.-p2 C.-1 D.1
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测二(解析版) 题型:选择题
阅读下面的程序框图,运行相应的程序,则输出S的值为( )

A.119 B.120 C.110 D.101
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测三(解析版) 题型:选择题
已知集合A={0,1},B={2},定义集合M={x|x=ab+a-b,a,b∈A或B},则M中所有元素之和为( )
A.7 B.0 C.-1 D.6
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科算法和程序框图(解析版) 题型:选择题
运行如下程序框图,如果输入的t∈[-1,3],则输出s属于 ( )

A.[-3,4]
B.[-5,2]
C.[-4,3]
D.[-2,5]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com