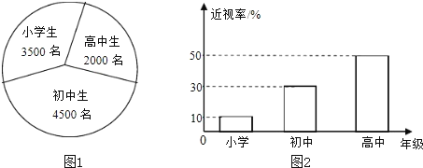
[题目]已知某地区中小学生人数和近视情况分别如图1和图2所示.为了解该地区中小学生的近视形成原因.用分层抽样的方法抽取2%的学生进行调查.则样本容量和抽取的高中生近视人数分别是( )A.100.10B.100.20C.200.10D.200.20 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知某地区中小学生人数和近视情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别是（）

A.100，10B.100，20C.200，10D.200，20

【答案】D

【解析】

根据图1可得总体个数，根据抽取比例可得样本容量，计算分层抽样的抽取比例，求得样本中的高中学生数，再利用图2求得样本中抽取的高中学生近视人数．

由图1知：总体个数为3500+2000+4500=10000，

∴样本容量=10000×2%=200，

分层抽样抽取的比例为，

∴高中生抽取的学生数为2000×=40人，

∴抽取的高中生近视人数为40×50%=20人.

故选：D.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知△ABC的三个顶点分别为A（﹣3，0），B（2，1），C（﹣2，3），试求：

（1）边AC所在直线的方程；

（2）BC边上的中线AD所在直线的方程；

（3）BC边上的高AE所在直线的方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在正四棱锥S－ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论：①EP⊥AC；②EP∥BD；③EP∥平面SBD；④EP⊥平面SAC，其中恒成立的为( )

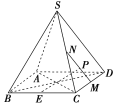
A.①③B.③④C.①②D.②③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的左、右焦点在轴上，中心在坐标原点，长轴长为4，短轴长为.

（1）求椭圆的标准方程；

（2）是否存在过的直线，使得直线与椭圆交于，？若存在，请求出直线的方程；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知四边形ABCD由Rt△ABC和Rt△BCD拼接而成，其中∠BAC＝∠BCD＝90°，∠DBC＝30°，AB＝AC，，将△ABC沿着BC折起，

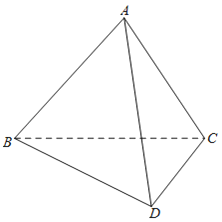
（1）若，求异面直线AB和CD所成角的余弦值；

（2）当四面体ABCD的体积最大时，求二面角A﹣BC﹣D的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】现有分别写有1，2，3，4，5的5张卡片．

（1）从中随机抽取2张，求两张卡片上数字和为5的概率；

（2）从中随机抽取1张，放回后再随机抽取1张，求抽得的第一张卡片上的数大于第二张卡片上的数的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】重庆近年来旅游业高速发展，有很多著名景点，如洪崖洞、磁器口、朝天门、李子坝等.为了解端午节当日朝天门景点游客年龄的分布情况，从年龄在22～52岁之间的旅游客中随机抽取了1000人，制作了如图的频率分布直方图.

（1）求抽取的1000人的年龄的平均数、中位数；（每一组的年龄取中间值）

（2）现从中按照分层抽样抽取8人，再从这8人中随机抽取3人，记这3人中年龄在的人数为，求的分布列及.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有一名高二学生盼望2020年进入某名牌大学学习，假设该名牌大学有以下条件之一均可录取：①2020年2月通过考试进入国家数学奥赛集训队（集训队从2019年10月省数学竞赛一等奖中选拔）：②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线，③2020年6月高考达到该校录取分数线（该校录取分数线高于重点线），该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表