
分析 把|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{13}$两边平方,代入向量的模,结合向量的数量积即可求得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,
由|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{13}$,得
$(\overrightarrow{a}-\overrightarrow{b})^{2}=|\overrightarrow{a}{|}^{2}-2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}=13$,
∴$|\overrightarrow{a}{|}^{2}-2|\overrightarrow{a}||\overrightarrow{b}|cosθ+|\overrightarrow{b}{|}^{2}=13$,
即16-2×4×3cosθ+9=13,
∴cosθ=$\frac{1}{2}$.
∵0°≤θ≤180°,
∴θ=60°.
点评 本题考查平面向量的数量积运算,训练了利用数量积求向量的夹角,是中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
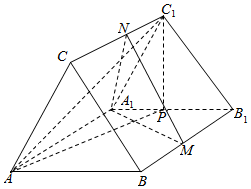 如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.
如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=1,b=1 | B. | a=3,b=1 | C. | a=1,b=0 | D. | a=3,b=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com