练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．在平面直角坐标系xOy中，已知四边形ABCD是平行四边形，$\overrightarrow{AB}$=（3，1），$\overrightarrow{AD}$=（2，-2），则$\overrightarrow{AC}•\overrightarrow{BD}$（　　）
    A．2B．-2C．-10D．10

    分析 求出$\overrightarrow{AC}，\overrightarrow{BD}$的坐标，再计算数量积．

    解答 解：$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$=（5，-1），$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$=（-1，-3）．
    ∴$\overrightarrow{AC}•\overrightarrow{BD}$=5×（-1）+（-1）×（-3）=-2．
    故选B．

    点评 本题考查了平面向量的坐标运算，数量级运算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

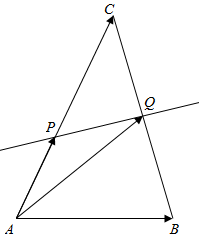    5．如图，已知△ABC的边BC的垂直平分线交AC于点P，交BC于点Q，若|$\overrightarrow{AB}$|=3，|$\overrightarrow{AC}$|=5，则（$\overrightarrow{AP}$+$\overrightarrow{AQ}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）的值为-16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知圆x2+y2=17在点（1，4）处的切线与幂函数f（x）的图象在点A（1，f（1））处的切线垂直，且不等式$\frac{f（x）}{x}$＞ax2+x在（1，2）上能成立，则实数a的取值范围为（　　）
    A．[0，+∞）B．（$\frac{35}{6}$，+∞）C．（-∞，0]D．（-∞，$\frac{3}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．方程cos2x=cosx在[0，2π]内的解集为{0，2π，$\frac{2π}{3}$，$\frac{4π}{3}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}-5，x≥0}\\{3+{x}^{2}，x＜0}\end{array}\right.$，则f[f（2）]=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知f（x）=cosx•cos2x•cos4x，若f（α）=$\frac{1}{8}$，则角α不可能等于（　　）
    A．$\frac{π}{9}$B．$\frac{2π}{9}$C．$\frac{2π}{7}$D．$\frac{4π}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列表述正确的是（　　）
    A．过平面β外一点可以作无数条直线与平面β平行
    B．过直线l外一点可作无数条直线平行于l
    C．垂直于两条异面直线的空间直线只有一条
    D．空间三个平面最多把空间分成七部分

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．（普通中学做）已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）以及双曲线C2：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线将第一象限三等分，则C1，C2的离心率之积为（　　）
    A．$\frac{4\sqrt{3}}{3}$B．$\frac{4}{3}$或4C．$\frac{4}{3}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知F1（-1，0），F2（1，0）是椭圆C1与双曲线C2共同的焦点，椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，椭圆C1与双曲线C2的离心率分别为e1，e2，则e1+e2取值范围为（　　）
    A．[2，+∞）B．[4，+∞）C．（4，+∞）D．（2，+∞）

    查看答案和解析>>

    同步练习册答案