
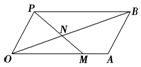
 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.分析 (1)利用$\frac{OM}{PB}=\frac{ON}{BN}$得出方程得出f(x);
(2)对Sn=f(Sn-1)=$\frac{{S}_{n-1}}{1+{S}_{n-1}}$取倒数,即可得出{$\frac{1}{{S}_{n}}$}为等差数列,从而求出Sn,再利用an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$.
解答 解:(1)∵$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$,
∴$\frac{ON}{BN}$=x,$\frac{ON}{OB}=y$,∴$\frac{ON}{BN}=\frac{y}{1-y}$,
∵△OMN∽△BPN,
∴$\frac{OM}{PB}=\frac{ON}{BN}$,
∴$\frac{y}{1-y}=x$,
∴y=f(x)=$\frac{x}{1+x}$.
(2)Sn=f(Sn-1)=$\frac{{S}_{n-1}}{1+{S}_{n-1}}$,
∴$\frac{1}{{S}_{n}}$=$\frac{1+{S}_{n-1}}{{S}_{n-1}}$,∴$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=1,
∵S1=a1=1,∴数列{$\frac{1}{{S}_{n}}$}是首项为1,公差为1的等差数列,
∴$\frac{1}{{S}_{n}}$=n,即Sn=$\frac{1}{n}$,
当n≥2时,an=Sn-Sn-1=$\frac{1}{n}$-$\frac{1}{n-1}$=$\frac{1}{n-{n}^{2}}$.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{n-{n}^{2}},n≥2}\end{array}\right.$.
点评 本题考查向量知识的运用,考查向量共线的条件,考查等差数列的证明,考查求数列的通项,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com