
分析 (1)由an+an+1=6•5n,an+1+an+2=6•5n+1,得到等比数列(an}的公比q=5,由此能求出t的值.
(2)an+an+1+an+2+…+an+k=6pn,an+1+an+2+an+3+…+an+1+k=6pn+1,数列{an}是一个等比数列,所以求出公比为p,由此能求出t.
(3)由Tn=a1+$\frac{{a}_{2}}{p}$+$\frac{{a}_{3}}{{p}^{2}}$+…+$\frac{{a}_{n-1}}{{p}^{n-2}}$+$\frac{{a}_{n}}{{p}^{n-1}}$,$\frac{1}{p}$Tn=a1+$\frac{{a}_{1}+{a}_{2}}{p}$+$\frac{{a}_{2}+{a}_{3}}{{p}^{2}}$+…+$\frac{{a}_{n-1}+{a}_{n}}{{p}^{n-1}}$+$\frac{{a}_{n}}{{p}^{n}}$,由此能够证明 $\frac{1+p}{p}$Tn-$\frac{{a}_{n}}{{p}^{n}}$-6n=a1-6=-5.
解答 解:(1)an+an+1=6•5n,
an+1+an+2=6•5n+1,…(2分)
设等比数列(an}的公比是q,
则an+an+1=6•5n•5,
∴q=5,…(4分)
n=1时,t+5t=30,∴t=5.…(5分)
(2)an+an+1+an+2+…+an+k=6pn,
an+1+an+2+an+3+…+an+1+k=6pn+1,…(6分)
数列{an}是一个等比数列,所以求出公比为p,…(7分)
∴t(pn-1+pn+…+pn+k-1)=6pn,…(8分)
项数为n+k-1-(n-1)十1=k+1项,
当p=1时,t(k+1)=6,
∴t=$\frac{6}{k+1}$,…(9分)
当p≠1,且p>0时,t $\frac{{p}^{n-1}(1-{p}^{k+1})}{1-p}$=6pn,
∴t=$\frac{6p(1-p)}{1-{p}^{k+1}}$..…(10分)
(3)证明:∵n是任意的正整数,当n=1时,$\frac{{a}_{1}+{a}_{2}}{p}$=6P1=6,
依此类推,当n取n-1项时,$\frac{{a}_{n-1}+{a}_{n}}{{p}^{n-1}}$=$\frac{6{p}^{n}}{{p}^{n-1}}$=6,
∴Tn=a1+$\frac{{a}_{2}}{p}$+$\frac{{a}_{3}}{{p}^{2}}$+…+$\frac{{a}_{n-1}}{{p}^{n-2}}$+$\frac{{a}_{n}}{{p}^{n-1}}$,
$\frac{1}{p}$Tn=$\frac{{a}_{1}}{p}$+$\frac{{a}_{2}}{{p}^{2}}$+$\frac{{a}_{3}}{{p}^{3}}$+…+$\frac{{a}_{n-1}}{{p}^{n-2}}$+$\frac{{a}_{n}}{{p}^{n}}$=a1+$\frac{{a}_{1}+{a}_{2}}{p}$+$\frac{{a}_{2}+{a}_{3}}{{p}^{2}}$+…+$\frac{{a}_{n-1}+{a}_{n}}{{p}^{n-1}}$+$\frac{{a}_{n}}{{p}^{n}}$,…(12分)
∴(1+$\frac{1}{p}$)Tn=2a1+$\frac{{a}_{1}+2{a}_{2}}{p}$+$\frac{{a}_{2}+2{a}_{3}}{{p}^{2}}$+…+$\frac{{a}_{n-1}+2{a}_{n}}{{p}^{n-1}}$+$\frac{{a}_{n}}{{p}^{n}}$=a1+6n-6+$\frac{{a}_{n}}{{p}^{n}}$,…(14分)
∴$\frac{1+p}{p}$Tn-$\frac{{a}_{n}}{{p}^{n}}$-6n=a1-6=-5.…(17分)
点评 本题考查数列的综合运用,综合性强,难度大,对数学思维的要求较高,有一定的探索性,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
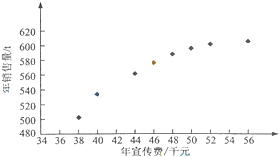 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到如图的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到如图的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
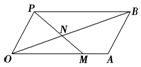 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com