Question

【题目】已知函数.

（1）当时，求函数的单调区间；

（2）当时，若函数在上的最小值为0，求的值；

（3）当时，若函数在上既有最大值又有最小值，且恒成立，求实数的取值范围.

Answer 1

【答案】（1）单调递减区间为；（2）或；（3）或.

【解析】

（1）将代入函数解析式，去掉绝对值符号，将函数写出分段函数的形式，结合二次函数的单调性，写出函数的单调递减区间；

（2）将函数解析式化为分段函数的形式，对的范围进行讨论，从而确定函数的最小值点，相互对照，求得结果；

（3）首先根据题意，判断出函数在区间上存在最值的条件，利用恒成立，转化得出对应的不等关系，进而求得其范围.

（1）当时，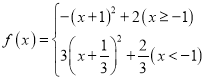

由二次函数单调性知在单调递减，在单调递减，

∴的单调递减区间为

（2）

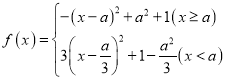
当时，在单调递减，单调递增，单调递减，

（i）当即时，

∴（舍去）

（ii）由得

当，即时，

∴，符合题意.

（iii）当，即时，

∴，符合题意.

综上所述，或.

（3）当时，由，可知

由可知

要使恒成立

∵

又∵

∴，∴

∴或.