
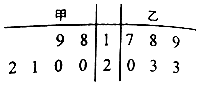
 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.分析 (1)根据茎叶图中的数据,计算甲、乙的中位数和众数即可;
(2)计算甲、乙的平均数和方差,比较即可得出结论.
解答 解:(1)根据茎叶图知,
甲的中位数为$\frac{20+20}{2}=20$,众数为20;
乙的中位数为$\frac{19+20}{2}=19.5$,众数为23;
(2)计算甲的平均数为$\overline{x_甲}=\frac{18+19+20+20+21+22}{6}=20$,
方差为$S_甲^2=\frac{{{{({18-20})}^2}+{{({19-20})}^2}+{{({20-20})}^2}+{{({20-20})}^2}+{{({21-20})}^2}+{{({22-20})}^2}}}{6}=\frac{5}{3}$,
乙的平均数是$\overline{x_乙}=\frac{17+18+19+20+23+23}{6}=20$,
方差是$S_乙^2=\frac{{{{({17-20})}^2}+{{({18-20})}^2}+{{({19-20})}^2}+{{({20-20})}^2}+{{({23-20})}^2}+{{({23-20})}^2}}}{6}=\frac{16}{3}$,
由于$\overline{x_甲}=\overline{x_乙}$,且$S_甲^2<S_乙^2$,
所以甲更为优秀.
点评 本题考查了根据茎叶图中的数据,计算中位数、众数、平均数和方差的应用问题,是基础题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | 2016×2017 | B. | 20172 | C. | 2017×2018 | D. | 2018×2019 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
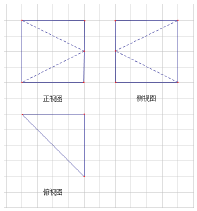 图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )| A. | 32π | B. | 48π | C. | 50π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com