
分析 (1)2$\sqrt{S_n}={a_n}$+1,可得4Sn=$({a}_{n}+1)^{2}$,n≥2时,4Sn-1=$({a}_{n-1}+1)^{2}$,相减可得:(an+an-1)(an-an-1-2)=0.于是∴an-an-1=2.利用等差数列的通项公式即可得出.
(2)bn=(-1)n-1an=(-1)n-1(2n-1).对n分类讨论即可得出.
(3)cn=$\frac{1}{{\sqrt{{a_n}{S_{2n+1}}}+\sqrt{{a_{n+1}}{S_{2n-1}}}}}$=$\frac{1}{(2n+1)\sqrt{2n-1}+(2n-1)\sqrt{2n+1}}$=$\frac{1}{2}(\frac{1}{\sqrt{2n-1}}-\frac{1}{\sqrt{2n+1}})$,
可得$\sum_{i=1}^n{[{({\sqrt{2n+1}+1}){c_i}}]}$=$(\sqrt{2n+1}+1)$×$\frac{1}{2}(1-\frac{1}{\sqrt{2n+1}})$=$\frac{n}{\sqrt{2n+1}}$.再利用单调性即可得出.
解答 解:(1)∵2$\sqrt{S_n}={a_n}$+1,∴4Sn=$({a}_{n}+1)^{2}$,
n≥2时,4Sn-1=$({a}_{n-1}+1)^{2}$,∴4an=$({a}_{n}+1)^{2}$-$({a}_{n-1}+1)^{2}$,
化为:(an+an-1)(an-an-1-2)=0.
∵an+an-1>0,∴an-an-1=2.
n=1时,4a1=$({a}_{1}+1)^{2}$,解得a1=1.
∴数列{an}是等差数列,公差为2.
∴an=1+2(n-1)=2n-1.
(2)∵bn=(-1)n-1an=(-1)n-1(2n-1).
n=2k为偶数时,b2k-1+b2k=(4k-3)-(4k-1)=-2.
∴数列{bn}的前n项和Tn=-2k=-n.
n=2k-1为奇数时,数列{bn}的前n项和Tn=Tn-1+bn=-(n-1)+(2n-1)=n.
综上可得:Tn=(-1)n-1n.
(3)cn=$\frac{1}{{\sqrt{{a_n}{S_{2n+1}}}+\sqrt{{a_{n+1}}{S_{2n-1}}}}}$=$\frac{1}{(2n+1)\sqrt{2n-1}+(2n-1)\sqrt{2n+1}}$=$\frac{1}{2}(\frac{1}{\sqrt{2n-1}}-\frac{1}{\sqrt{2n+1}})$,
∴$\sum_{i=1}^n{[{({\sqrt{2n+1}+1}){c_i}}]}$=$(\sqrt{2n+1}+1)$×$\frac{1}{2}(1-\frac{1}{\sqrt{2n+1}})$=$\frac{n}{\sqrt{2n+1}}$.
令dn=$\frac{n}{\sqrt{2n+1}}$>0,则$\frac{{d}_{n+1}^{2}}{{d}_{n}^{2}}$=$\frac{\frac{(n+1)^{2}}{2n+3}}{\frac{{n}^{2}}{2n+1}}$=$\frac{2{n}^{3}+5{n}^{2}+4n+1}{2{n}^{3}+3{n}^{2}}$>1.
可得dn+1>dn,因此数列{dn}单调递增.
∴dn≥d1=$\frac{\sqrt{3}}{3}$.
∴$\sum_{i=1}^n{[{({\sqrt{2n+1}+1}){c_i}}]}$的最小值是$\frac{\sqrt{3}}{3}$.
点评 本题考查了数列递推关系、等差数列的通项公式、裂项求和方法、分类讨论方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
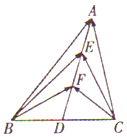 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
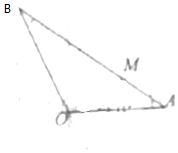 如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.
如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
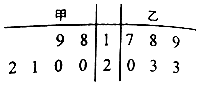 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com