考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件得a
n+2-a
n=6,由此能求出a
n=3n-1.
(2)由已知条件得数列{a
n}的奇数项是首项为3,公差为6的等差数列,偶数项是首项为4,公差为6的等差数列,从而得到
b2+b4+…+b2k=(1-+-+…+-)=,由此能示出存在正整数k,k=4,5.
解答:
(本题满分13分)
解:(1)∵a
n+a
n+1=6n+1,
∴a
n+1+a
n+2=6n+7,∴a
n+2-a
n=6,
又数列{a
n}是等差数列,设其公差为d,则2d=6,∴d=3,…(3分)
又a
1+a
2=7,∴2a
1+d=7,∴a
1=2,∴a
n=2+3(n-1)=3n-1,
故数列{a
n}的通项公式为
an=3n-1(n∈N*).…(6分)
(2)由 a
1+a
2=7,又a
1=3,得a
2=4,
由(1)知数列{a
n}的奇数项是首项为3,公差为6的等差数列,
偶数项是首项为4,公差为6的等差数列.…(8分)
S2k=3k+×6+4k+×6=6k2+k,
∴
b2k====(-)…(10分)
∴
b2+b4+…+b2k=(1-+-+…+-)=,
解不等式
<<,得3<k<6
又k为正整数,故存在正整数k,k=4,5.…(13分)
点评:本题考查数列的通项公式的求法,考查满足条件的正整数的求法,是中档题,解题时要注意挖掘隐含条件,注意裂项求和法的合理运用.



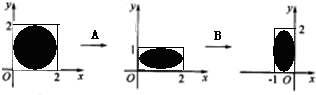 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.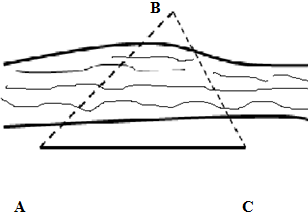 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.