Question

已知函数.
（1）求的单调区间；
（2）记为的从小到大的第个零点，证明：对一切，有.

Answer 1

(1) 单调递减区间为,
单调递增区间为.(2)详见解析

解析试题分析:(1)对函数求导得到导函数,求大于0和小于0的解集得到单调减区间和单调增区间,但是必须注意正余弦的周期性和原函数的定义域.
(2)利用(1)问的结果可知函数在区间上是单调递减的,即在区间上至多一个零点,根据正余弦的函数值可得,再根据在区间上单调性和函数在区间端点处函数值异号可得函数在区间上有且只有一个零点,即,则依次讨论利用放缩法即可证明.
数求导可得,令可得
,当时,.此时;
当时,,此时,
故函数的单调递减区间为,
单调递增区间为.
(2)由(1)可知函数在区间上单调递减,又,所以,
当时,因为,且函数的图像是连续不断的,所以在区间内至少存在一个零点,又在区间上是单调的,故,因此,
当时,;
当时,;
当时,


,
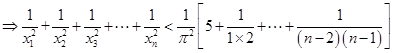
综上所述,对一切的,.
考点：导数 单调性 放缩法 裂项求和