
分析 (1)由(x1-x2)2=(x1+x2)2-4x1x2,利用韦达定理能求出|x1-x2|.
(2)由$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,利用韦达定理能求出结果.
(3)由x12+x22=(x1+x2)2-2x1x2,利用韦达定理能求出结果.
解答 解:(1)∵x1和x2分别是一元二次方程x2+4x-3=0的两个根,
∴x1+x2=-4,x1x2=-3,
∴(x1-x2)2=(x1+x2)2-4x1x2=16+12=28,
∴|x1-x2|=$\sqrt{28}=2\sqrt{7}$.
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-4}{-3}$=$\frac{4}{3}$.
(3)x12+x22=(x1+x2)2-2x1x2=16+6=22.
点评 本题考查代数式化简求值,是基础题,解题时要认真审题,注意韦达定理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
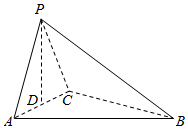 如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.
如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l∥m且l⊥平面α | B. | l⊥m且l∥平面α | C. | l⊥m且l⊥平面α | D. | l∥m且l∥平面α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
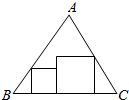 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com