设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左.右焦点为F1.F2.过点F1的直线与椭圆C相交于A.B两点.若$\overrightarrow{A{F} {1}}$=$\frac{3}{2}$$\overrightarrow{{F} {1}B}$.∠AF2B=90°.则椭圆C的离心率是$\frac{\sqrt{5}}{5}$� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

1．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点为F₁，F₂，过点F₁的直线与椭圆C相交于A，B两点，若$\overrightarrow{A{F}_{1}}$=$\frac{3}{2}$$\overrightarrow{{F}_{1}B}$，∠AF₂B=90°，则椭圆C的离心率是$\frac{\sqrt{5}}{5}$．

分析由条件可设|BF₁|=2t，|AF₁|=3t，由椭圆的定义，可得|AF₂|=2a-3t，|BF₂|=2a-2t，运用勾股定理，可得t=$\frac{1}{3}$a，求出cosB，△F₁BF₂中，运用余弦定理和离心率公式计算即可得到所求值．

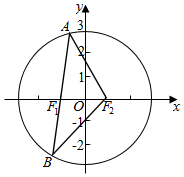解答解：由$\overrightarrow{A{F}_{1}}$=$\frac{3}{2}$$\overrightarrow{{F}_{1}B}$，可设|BF₁|=2t，|AF₁|=3t，
由椭圆的定义，可得|AF₂|=2a-3t，|BF₂|=2a-2t，
由∠AF₂B=90°可得|AB|²=|AF₂|²+|BF₂|²，
即有（5t）²=（2a-3t）²+（2a-2t）²，
解得t=$\frac{1}{3}$a，|AB|=$\frac{5}{3}$a，|BF₂|=$\frac{4}{3}$a，
在△ABF₂中，cosB=$\frac{|B{F}_{2}|}{|AB|}$=$\frac{4}{5}$，
在△F₁BF₂中，cosB=$\frac{\frac{4}{9}{a}^{2}+\frac{16}{9}{a}^{2}-4{c}^{2}}{2•\frac{2}{3}a•\frac{4}{3}a}$=$\frac{4}{5}$，
化简可得$\frac{9}{4}$•$\frac{{c}^{2}}{{a}^{2}}$=$\frac{9}{20}$，
即e²=$\frac{1}{5}$，即为e=$\frac{\sqrt{5}}{5}$．
故答案为：$\frac{\sqrt{5}}{5}$．

点评本题考查椭圆的离心率的求法，注意运用椭圆的定义，三角形的勾股定理和余弦定理，考查向量共线定理，考查化简整理的运算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

11．已知函数f（x）=ax-lnx，当x∈（0，e]（e为自然常数）时，函数f（x）的最小值为3，则a的值为（　　）

A．

B．

e²

C．

D．

2e²

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$的四个顶点构成一个面积为$2\sqrt{3}$的四边形，该四边形的一个内角为60°．
（Ⅰ）求椭圆E的方程；
（Ⅱ）直线l与椭圆E相交于A，B两个不同的点，线段AB的中点为C，O为坐标原点，若△OAB面积为$\frac{{\sqrt{3}}}{2}$，求|AB|•|OC|的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{1}{2}$，且经过点$P（1，\frac{3}{2}）$，两个焦点分别为F₁，F₂．
（1）求椭圆C的方程；
（2）过F₁的直线l与椭圆C相交于A，B两点，若△AF₂B的内切圆半径为$\frac{{3\sqrt{2}}}{7}$，求以F₂为圆心且与直线l相切的圆的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．袋中有5只大小相同的乒乓球，编号为1至5，从袋中随机抽取3只，若以ξ表示取到球中的最大号码，则ξ的数学期望是$\frac{9}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．已知α，β表示两个不同平面，a，b表示两条不同直线，对于下列两个命题：
①若b?α，a?α，则“a∥b”是“a∥α”的充分不必要条件
②若a?α，b?α，则“α∥β”是“α∥β且b∥β”的充要条件．
判断正确的是（　　）

	A．	①，②是真命题		B．	①是真命题，②是假命题
	C．	①是假命题，②是真命题		D．	①，②都是假命题

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．已知集合A={0，1，2}，则集合B={x-y|x∈A，y∈A}的元素个数为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，上顶点为B，直线AB的斜率为$\frac{\sqrt{6}}{6}$，坐标原点O到直线AB的距离为$\frac{\sqrt{42}}{7}$．
（I）求椭圆C的标准方程；
（Ⅱ）是否在圆O：x²+y²=b²上存在点D，使得圆O过点D的切线与椭圆C交于点P，Q，线段PQ的中点为M，直线PQ与OM的夹角为45°？若存在，求点D的横坐标；若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．已知全集U={1，2，3，4，5}，集合A={1，2，3}，B={3，4，5}，则A∩∁_UB=（　　）

A．

{3}

B．

{1，2，4，5}

C．

{1，2}

D．

{1，3，5}

查看答案和解析>>

同步练习册答案