Question

20．点O是△ABC所在平面上一点，且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$，则点O为△ABC的（　　）

• A． 外心
• B． 内心
• C． 重心
• D． 垂心

Answer 1

分析 作BD∥OC，CD∥OB，连结OD，OD与BC相交于G，可得$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$，又$\overrightarrow{OB}$+$\overrightarrow{OC}$=-$\overrightarrow{OA}$，从而可得$\overrightarrow{OD}$=-$\overrightarrow{OA}$，即AG是BC边上的中线，同理可证BO，CO的延长线也为△ABC的中线，即O为三角形ABC的重心．

解答 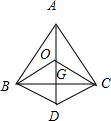解：作BD∥OC，CD∥OB，连结OD，OD与BC相交于G，则BG=CG，（平行四边形对角线互相平分），
∴$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$，
又∵$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$，可得：$\overrightarrow{OB}$+$\overrightarrow{OC}$=-$\overrightarrow{OA}$，
∴$\overrightarrow{OD}$=-$\overrightarrow{OA}$，
∴A，O，G在一条直线上，可得AG是BC边上的中线，
同理：BO，CO的延长线也为△ABC的中线．
∴O为三角形ABC的重心．
故选：C．

点评 本题主要考查了向量在几何中的应用，以及向量的基本运算，同时考查了转化思想和数形结合思想，属于中档题．