
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 由题意知本题是一个几何概型,根据所给的条件作出试验发生是包含的所有事件是一个矩形区域,做出面积,看出满足条件的事件对应的面积,根据几何概型公式得到结果.
解答 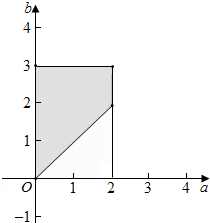 解:如图,所有的基本事件对应集合Ω={(a,b)|0≤a≤2,0≤b≤3},
解:如图,所有的基本事件对应集合Ω={(a,b)|0≤a≤2,0≤b≤3},
所构成的区域为矩形及其内部,其面积为S=3×2=6,
事件A对应的集合A={(a,b)|0≤a≤2,0≤b≤3,且a<b},
且在直线a=b的右上方部分,其面积S'=6-$\frac{1}{2}$×2×2=4,
故事件A发生的概率P(A)=$\frac{4}{6}$=$\frac{2}{3}$,
故选:A.
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.


科目:高中数学 来源: 题型:解答题
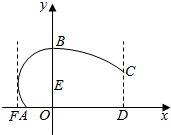 某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).
某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
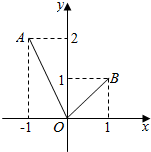 如图,定义在[-1,1]上的函数f(x)的图象为折线AOB.若方程f(x)-mx-m=0有两个不等的实根,则实数m的取值范围是(0,$\frac{1}{2}$].
如图,定义在[-1,1]上的函数f(x)的图象为折线AOB.若方程f(x)-mx-m=0有两个不等的实根,则实数m的取值范围是(0,$\frac{1}{2}$].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com