
| A. | 36 | B. | 40 | C. | 44 | D. | 48 |
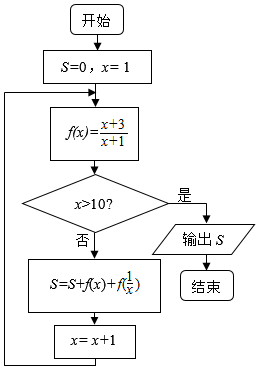
分析 模拟执行程序框图,依次写出每次循环得到的S,x,f(x)的值,观察S的取值规律,当x=11时满足条件x>10,退出循环,输出S的值,即可得解.
解答 解:模拟执行程序框图,可得
S=0,x=1
f(x)=2,
不满足条件x>10,S=4,x=2,f(x)=$\frac{5}{3}$,
不满足条件x>10,S=4+$\frac{5}{3}$+$\frac{7}{3}$=8,x=3,f(x)=$\frac{3}{2}$,
不满足条件x>10,S=8+$\frac{3}{2}$+$\frac{5}{2}$=12,x=4,f(x)=$\frac{7}{5}$,f($\frac{1}{x}$)=$\frac{13}{5}$,
不满足条件x>10,S=12+$\frac{7}{5}$+$\frac{13}{5}$=16,x=5,f(x)=$\frac{4}{3}$,f($\frac{1}{x}$)=$\frac{8}{3}$,
不满足条件x>10,S=16+$\frac{4}{3}$+$\frac{8}{3}$=20,x=6,f(x)=$\frac{9}{7}$,f($\frac{1}{x}$)=$\frac{19}{7}$,
不满足条件x>10,S=20+$\frac{9}{7}$+$\frac{19}{7}$=24,x=7,f(x)=$\frac{5}{4}$,f($\frac{1}{x}$)=$\frac{11}{4}$,
不满足条件x>10,S=24+$\frac{5}{4}$+$\frac{11}{4}$=28,x=8,…
观察规律可得:
不满足条件x>10,S=32,x=9,…
不满足条件x>10,S=36,x=10,…
不满足条件x>10,S=40,x=11,…
满足条件x>10,退出循环,输出S的值为40.
故选:B.
点评 本题主要考查了循环结构的程序框图,正确写出每次循环得到的S,x,f(x)的值,观察S的取值规律是解题的关键,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 垂直 | C. | 相交不垂直 | D. | 无法判定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的离心率大于1 | |
| B. | 双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=-1$的焦点在x轴上 | |
| C. | $?x∈R,sinx+cosx=\frac{7}{5}$ | |
| D. | 不等式$\frac{1}{x}>1$的解集为(-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±3x | B. | y=±$\sqrt{3}$x | C. | y=±x | D. | y=±$\frac{\sqrt{3}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com