
证明不等式 (n∈N*)
(n∈N*)
见解析
【解析】
试题分析:证法一:利用数学归纳法证明(1)当n=1时,验证不等式成立;(2)假设n=k(k≥1)时,不等式成立,然后证明当n=k+1时,不等式也成立.即可.
证法二:构造函数f(n)=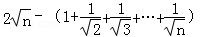 ,通过函数单调性定义证明f(k+1)>f(k)
,通过函数单调性定义证明f(k+1)>f(k)
然后推出结论.
证法一:(1)当n=1时,不等式左端=1,右端=2,所以不等式成立;
(2)假设n=k(k≥1)时,不等式成立,即1+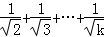 <2
<2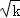 ,
,
则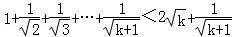
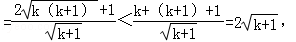
∴当n=k+1时,不等式也成立.
综合(1)、(2)得:当n∈N*时,都有1+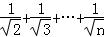 <2
<2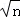 .
.
证法二:设f(n)=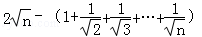 ,
,
那么对任意k∈N?* 都有:
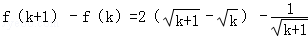
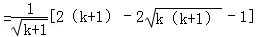
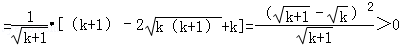
∴f(k+1)>f(k)
因此,对任意n∈N* 都有f(n)>f(n﹣1)>…>f(1)=1>0,
∴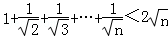 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:填空题
若m是一个给定的正整数,如果两个整数a、b用m除所得的余数相同,则称a与b对m校同余,记作a≡b[mod(m)],例如7≡16[mod(3)],若22014≡r[mod(7)],则r可能为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型:选择题
下列各组关于最大公约数的说法中不正确的是( )
A.16和12的最大公约数是4
B.78和36的最大公约数是6
C.85和357的最大公约数是34
D.105和315的最大公约数是105
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
存在整数n,使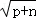 +
+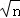 是整数的质数p( )
是整数的质数p( )
A.不存在
B.只有一个
C.多于一个,但为有限个
D.有无穷多个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例(解析版) 题型:填空题
用数学归纳法证明“(n+1)(n+2)…(n+n)=2n•1•2•…•(2n﹣1)”(n∈N+)时,从“n=k到n=k+1”时,左边应增添的式子是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
一个关于自然数n的命题,如果验证当n=1时命题成立,并在假设当n=k(k≥1且k∈N*)时命题成立的基础上,证明了当n=k+2时命题成立,那么综合上述,对于( )
A.一切正整数命题成立 B.一切正奇数命题成立
C.一切正偶数命题成立 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
(2014•河西区三模)用数学归纳法证明1+2+3+…+n3=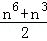 ,则当n=k+1时,左端应在n=k的基础上加上( )
,则当n=k+1时,左端应在n=k的基础上加上( )
A.k3+1
B.(k+1)3
C.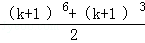
D.(k3+1)+(k3+2)+(k3+3)+…+(k3+1)3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷(解析版) 题型:选择题
用反证法证明命题:“若a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A.a,b都能被3整除 B.a,b都不能被3整除
C.a,b不都能被3整除 D.a不能被3整除
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com