
分析 (Ⅰ)由$\left\{\begin{array}{l}f'(0)=5\\ f(1)+f'(1)=12\end{array}\right.$,得$\left\{\begin{array}{l}a+b=5\\ a{e^a}+b+b+{e^a}=12\end{array}\right.$,化简得a,b,利用导数求极值.
(Ⅱ)f(x)>x2+3在x∈[1,m]上恒成立,等价于e-x-x2+6x-3>0在x∈[1,m]上恒成立.设g(x)=e-x-x2+6x-3.求出其导函数,讨论导函数的符号,求出g(x)的最小值,最小值大于等于0,求出m的范围.
解答 解:(Ⅰ)f(x)=eax+bx,那么f'(x)=aeax+b,
由$\left\{\begin{array}{l}f'(0)=5\\ f(1)+f'(1)=12\end{array}\right.$,得$\left\{\begin{array}{l}a+b=5\\ a{e^a}+b+b+{e^a}=12\end{array}\right.$,化简得(ea-2)(a+1)=0
由a<0得a=-1,b=6,∴f(x)=e-x+6x…(3分)
即f'(x)=-e-x+6=0,得x=-ln6,
∴f(x)在(-∞,-ln6)单调递减,在(-ln6,+∞)单调递增,
∴$f{(x)_{极小值}}=f(-ln6)={e^{ln6}}-6ln6=6-6ln6$,无极大值.…(5分)
(Ⅱ)f(x)>x2+3在x∈[1,m]上恒成立,等价于e-x-x2+6x-3>0在x∈[1,m]上恒成立.
设g(x)=e-x-x2+6x-3,则g'(x)=-e-x-2x+6
设h(x)=g'(x)=-e-x-2x+6,则h'(x)=e-x-2,…(6分)
∵1≤x≤m,有h'(x)<0,∴h(x)在区间[1,m]上是减函数,
又∵h(1)=4-e-1>0,h(2)=2-e-2>0,h(3)=-e-3<0,
∴存在x0∈(2,3),使得h(x0)=g'(x0)=0,
当1≤x<x0时,有g'(x)>0,当x>x0时,有g'(x)<0.
∴y=g(x)在区间[1,x0]上递增,在区间(x0,m)上递减,
又∵g(1)=e-1+2>0,g(2)=e-2+5>0,g(3)=e-3+6>0,
g(4)=e-4+5>0,g(5)=e-5+2>0,g(6)=e-6-3<0.
∴当1≤x≤5时,恒有g(x)>0;当x≥6时,恒有g(x)<0;
∴正整数m的最大值为5.…(12分)
点评 本题考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
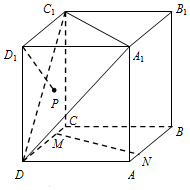 在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 抛物线的一部分 | D. | 双曲线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )
如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )| A. | 直线AC与直线EC′所成角为45° | |
| B. | 点E到平面OCD′的距离为$\frac{1}{2}$ | |
| C. | 四面体O EA′B′在平面ABCD上的射影是面积为$\frac{1}{6}$的三角形 | |
| D. | 过点O,E,C的平面截正方体所得截面的面积为$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com