
���� ��1��������ɵõ�4�µı�����ΪQ=��a1-b1��+��a2-b2��+��a3-b3��+��a4-b4����������㼴�ɵõ�����ֵ��
��2�����㵱n��4ʱ��Q=935+��-10��5+470��-��5+5��+��+��-10n+470��-��n+5����Ӧ�õȲ����е����ʽ�����������ɵ�Q�����ɶ��κ��������ʣ��ɵ�Q�����ֵ�������ʱ���г�ͣ�ŵ����ɳ������Ƚϼ��ɵõ����ۣ�
��� �⣺��1��an=$\left\{\begin{array}{l}{5{n}^{4}+15��n��[1��3]}\\{-10n+470��n��[4��+�ޣ�}\end{array}\right.$��n��N*��bn=n+5��n��N*����
�ɵõ�4�µı�����ΪQ=��a1-b1��+��a2-b2��+��a3-b3��+��a4-b4��
=��5+15-6��+��5��16+15-7��+��5��81+15-8��+��-40+470-9��=14+88+412+421=935��
��2����n��4ʱ��Q=935+��-10��5+470��-��5+5��+��+��-10n+470��-��n+5��
=935+��-10����$\frac{��n-4����n+5��}{2}$+470��n-4��-$\frac{��n-4����n+5��}{2}$-5��n-4��
=-$\frac{11}{2}$n2+$\frac{919}{2}$n-815��
�ɵ�Q=$\left\{\begin{array}{l}{14��n=1}\\{102��n=2}\\{514��n=3}\\{-\frac{11}{2}{n}^{2}+\frac{919}{2}n-815��n��4}\end{array}\right.$��n��N*��
n��4ʱ�����ڶԳ���Ϊ-$\frac{919}{2��11}$��42������С��
��n=42ʱ��Qȡ�����ֵ8782��
��ʱ��S42=-��42-46��2+8800=8784��8782��
��Qȡ���ֵʱ��ͣ�ŵ������ɣ�
���� ���⿼�麯��ģ����ʵ�������е�Ӧ�ã�������κ�������ֵ��ע��nΪ��Ȼ�������黯�����������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
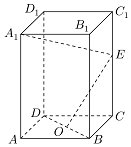 ��ͼ����������ABCD-A1B1C1D1�У�O��BD���е㣬E����CC1������һ�㣮
��ͼ����������ABCD-A1B1C1D1�У�O��BD���е㣬E����CC1������һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ��Բ | C�� | ˫���� | D�� | ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ABCD�DZ߳�Ϊ$2\sqrt{3}$�������Σ���E��F�ֱ��DZ�BC��CD���е㣬����ABE����CEF����ADF�ֱ���AE��EF��FA����ʹ��B��C��D�����غ��ڵ�P����������PAEF���ĸ�������ͬһ����������ϣ������ı�����ǣ�������
��ͼ��ABCD�DZ߳�Ϊ$2\sqrt{3}$�������Σ���E��F�ֱ��DZ�BC��CD���е㣬����ABE����CEF����ADF�ֱ���AE��EF��FA����ʹ��B��C��D�����غ��ڵ�P����������PAEF���ĸ�������ͬһ����������ϣ������ı�����ǣ�������| A�� | 6�� | B�� | 12�� | C�� | 18�� | D�� | $9\sqrt{2}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com