
分析 由题意画出几何体的图形,把A、B、C、D扩展为三棱柱,上下底面中心连线的中点与A的距离为球的半径,由此能求出球的体积.
解答 解:由题意画出几何体的图形,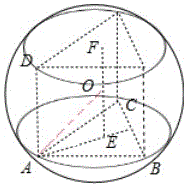 把A、B、C、D扩展为三棱柱,
把A、B、C、D扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
AD=2AB=6,OE=3,△ABC是正三角形,
∴AE=$\frac{2}{3}\sqrt{A{B}^{2}-(\frac{1}{2}AB)^{2}}$=$\sqrt{3}$,AO=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
∴球的体积为V=$\frac{4π}{3}(2\sqrt{3})^{3}$=32$\sqrt{3}π$.
故答案为:32$\sqrt{3}π$.
点评 本题考查球的表面积的求法,考查球、三棱柱等基础知识,考查推理论证能力、运算求解能力,考查函数与方思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
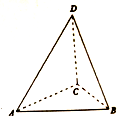 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )
如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )| A. | 直线AC与直线EC′所成角为45° | |
| B. | 点E到平面OCD′的距离为$\frac{1}{2}$ | |
| C. | 四面体O EA′B′在平面ABCD上的射影是面积为$\frac{1}{6}$的三角形 | |
| D. | 过点O,E,C的平面截正方体所得截面的面积为$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
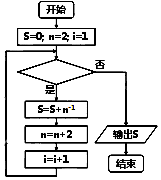
| A. | i>10 | B. | i<10 | C. | i<20 | D. | i>20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com