
 如图,ABCD是边长为$2\sqrt{3}$的正方形,点E,F分别是边BC,CD的中点,将△ABE,△CEF,△ADF分别沿AE,EF,FA折起,使得B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球的球面上,则该球的表面积是( )
如图,ABCD是边长为$2\sqrt{3}$的正方形,点E,F分别是边BC,CD的中点,将△ABE,△CEF,△ADF分别沿AE,EF,FA折起,使得B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球的球面上,则该球的表面积是( )| A. | 6π | B. | 12π | C. | 18π | D. | $9\sqrt{2}π$ |
分析 由已知得PA、PF、PE两两垂直,且PA=2$\sqrt{3}$,PE=PF=$\sqrt{3}$,以PA、PE、PF为棱构造一个长方体,则四面体PAEF的四个顶点在这个长方体的外接球上,由此能求出该球的表面积.
解答 解:∵ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,
将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,
∴PA、PF、PE两两垂直,且PA=2$\sqrt{3}$,PE=PF=$\sqrt{3}$,
以PA、PE、PF为棱构造一个长方体,
则四面体PAEF的四个顶点在这个长方体的外接球上,
∴这个球的半径为R=$\frac{\sqrt{3+3+12}}{2}$=$\frac{3\sqrt{2}}{2}$,
∴该球的表面积是S=4πR2=4π×$\frac{9}{2}$=18π.
故选:C.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意球、四面体的性质及构造法的合理应用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
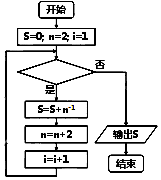
| A. | i>10 | B. | i<10 | C. | i<20 | D. | i>20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
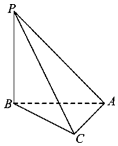 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )| A. | 3π | B. | 5π | C. | 12π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $d≈\root{3}{{\frac{60}{31}V}}$ | B. | $d≈\root{3}{2V}$ | C. | $d≈\root{3}{{\frac{15}{8}V}}$ | D. | $d≈\root{3}{{\frac{21}{11}V}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
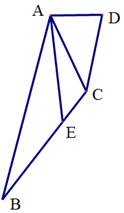 在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
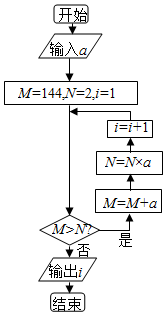 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com