
分析 (Ⅰ)求出函数的导数,得到f′(1)=0,求出a的值即可;
(Ⅱ)根据函数的奇偶性求出p,q的值,求出F(x)的解析式,求出函数的导数,从而求出函数的单调区间即可;
(Ⅲ)问题转化为λ(x-lnx)≤x2-2x在x∈[1,+∞)上恒成立,得到$λ≤\frac{{{x^2}-2x}}{x-lnx}$在x∈[1,+∞)上恒成立,令$φ(x)=\frac{{{x^2}-2x}}{x-lnx}({x≥1})$,根据函数的单调性求出λ的范围即可.
解答 解:(Ⅰ)由f(x)=ax3+x有f'(x)=3ax2+1
因为f(x)在x=1处取得极值,故f'(1)=3a+1=0
∴$a=-\frac{1}{3}$
经检验:当$a=-\frac{1}{3}$时,符合题意,故$a=-\frac{1}{3}$
(Ⅱ)由(Ⅰ)知:F(x)=(-x2+1)(x2+px+q)
∵F(x)的图象关于直线x=-1对称,故函数F(x-1)为偶函数
又F(x-1)=[-(x-1)2+1][(x-1)2+p(x-1)+q]=-x4+(4-p)x3+(3p-q-5)x2+2(1-p+q)x
∴$\left\{\begin{array}{l}4-p=0\\ 2({1-p+q})=0\end{array}\right.$,解得p=4,q=3
∴F(x)=(-x2+1)(x2+4x+3)
∴F'(x)=-2x(x2+4x+3)+(-x2+1)(2x+4)=-4(x+1)(x2+2x-1)
令F'(x)>0有$x<-1-\sqrt{2}$或$-1<x<-1+\sqrt{2}$
令F'(x)<0有$-1-\sqrt{2}<x<-1$或$x>-1+\sqrt{2}$
∴函数F(x)在区间$({-∞,-1-\sqrt{2}}),({-1,-1+\sqrt{2}})$上单调递增,
在区间$({-1-\sqrt{2},-1}),({-1+\sqrt{2},+∞})$上单调递减
(Ⅲ)由(Ⅱ)知,对任意的x≥1,都有g(x)≥(6+λ)x-λlnx+3恒成立,
可转化为λ(x-lnx)≤x2-2x在x∈[1,+∞)上恒成立
易知lnx<x∴$λ≤\frac{{{x^2}-2x}}{x-lnx}$在x∈[1,+∞)上恒成立
令$φ(x)=\frac{{{x^2}-2x}}{x-lnx}({x≥1})$,∴$φ'(x)=\frac{{({x-1})({x+2-2lnx})}}{{{{({x-lnx})}^2}}}$
令h(x)=x+2-2lnx(x≥1),∴$h'(x)=1-\frac{2}{x}$
∴h(x)在(1,2)上递减,(2,+∞)上递增
∴h(x)min=h(2)=4-2ln2>0
∴φ'(x)≥0,即φ(x)在[1,+∞)上递增
∴φ(x)min=φ(1)=-1
∴λ≤-1.
点评 本题考查了函数的奇偶性、单调性问题,考查导数的应用以及函数恒成立问题,是一道综合题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({-1,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
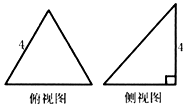 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )| A. | 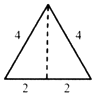 | B. | 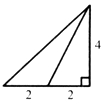 | C. | 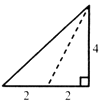 | D. | 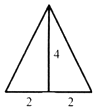 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
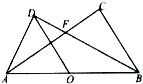 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com