
分析 (Ⅰ)当a1=2时,代入计算,可得a2;
(Ⅱ)利用反证法判断数列{an}不可能为等比数列;
(Ⅲ)利用数学归纳法进行证明.
解答 解:(Ⅰ)当a1=2时,${a_2}=\frac{2}{5}$;
(Ⅱ)设公比为q,则
∵${a_{n+1}}=\frac{a_n}{a_n^2+1}$,
∴${{a}_{n}}^{2}$+1=$\frac{1}{q}$,
∴q=1,此时an=0,矛盾
∴数列{an}不可能为等比数列;
(Ⅲ)n=1时,左边=a1,右边=$\frac{{a}_{1}-{a}_{2}}{{a}_{1}{a}_{2}}$=$\frac{{a}_{1}-\frac{{a}_{1}}{{{a}_{1}}^{2}+1}}{{a}_{1}•\frac{{a}_{1}}{{{a}_{1}}^{2}+1}}$=a1,成立;
假设n=k时,结论成立,则Sk=$\frac{{a}_{1}-{a}_{k+1}}{{a}_{1}{a}_{k+1}}$,
n=k+1时,左边=Sk+ak+1=$\frac{{a}_{1}-{a}_{k+1}}{{a}_{1}{a}_{k+1}}$+ak+1=$\frac{{a}_{1}-{a}_{k+1}+{a}_{1}{{a}_{k+1}}^{2}}{{a}_{1}{a}_{k+1}}$
右边=$\frac{{a}_{1}-{a}_{k+2}}{{a}_{1}{a}_{k+2}}$=$\frac{{a}_{1}-\frac{{a}_{k+1}}{{{a}_{k+1}}^{2}+1}}{{a}_{1}•\frac{{a}_{k+1}}{{{a}_{k+1}}^{2}+1}}$=$\frac{{a}_{1}-{a}_{k+1}+{a}_{1}{{a}_{k+1}}^{2}}{{a}_{1}{a}_{k+1}}$
∴左边=右边,
综上,${S_n}=\frac{{{a_1}-{a_{n+1}}}}{{{a_1}{a_{n+1}}}}$.
故答案为:$\frac{2}{5}$.
点评 本题考查数列的通项与求和,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (3,-1,-4) | B. | (-3,-1,-4) | C. | (3,1,4) | D. | (-3,-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
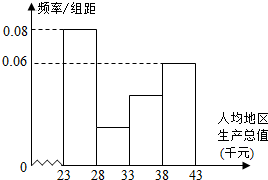 据我国西部各省(区、市)2013年人均地区生产总值(单位:千元)绘制的频率分布直方图如图所示,则人均地区生产总值在区间[28,38)上的频率是( )
据我国西部各省(区、市)2013年人均地区生产总值(单位:千元)绘制的频率分布直方图如图所示,则人均地区生产总值在区间[28,38)上的频率是( )| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com