
分析 (1)利用a1=$\frac{1}{2}$,an+1=$\frac{n{a}_{n}}{(n+1)(n{a}_{n}+1)}$,求a2,a3的值,设bn=$\frac{1}{n{a}_{n}}$,求数列{an}的通项公式;
(2)确定Sn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,$\frac{{S}_{n}}{{S}_{n+1}}$=$\frac{{n}^{2}+2n}{{n}^{2}+2n+1}$<1,再进行放缩,利用叠加法即可证明.
解答 (1)解:∵数列{an}中,a1=$\frac{1}{2}$,an+1=$\frac{n{a}_{n}}{(n+1)(n{a}_{n}+1)}$,
∴a2=$\frac{{a}_{1}}{2({a}_{1}+1)}$=$\frac{1}{6}$,a3=$\frac{2{a}_{2}}{3(2{a}_{2}+1)}$=$\frac{1}{12}$,
设bn=$\frac{1}{n{a}_{n}}$
∵an+1=$\frac{n{a}_{n}}{(n+1)(n{a}_{n}+1)}$,
∴bn+1-bn=1,
∵b1=2,
∴bn=2+n-1=n+1,
∴$\frac{1}{n{a}_{n}}$=n+1,
∴an=$\frac{1}{n(n+1)}$;
(2)证明:∵an=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴Sn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
∵$\frac{{S}_{n}}{{S}_{n+1}}$=$\frac{{n}^{2}+2n}{{n}^{2}+2n+1}$<1,
∴cn=(1-$\frac{{S}_{n}}{{S}_{n+1}}$)•$\frac{1}{\sqrt{{S}_{n+1}}}$=($\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n+1}}$)$\frac{{S}_{n}}{\sqrt{{S}_{n+1}}}$=($\frac{1}{\sqrt{{S}_{n}}}$-$\frac{1}{\sqrt{{S}_{n+1}}}$)($\frac{\sqrt{{S}_{n}}}{\sqrt{{S}_{n+1}}}$+$\frac{{S}_{n}}{{S}_{n+1}}$)<2($\frac{1}{\sqrt{{S}_{n}}}$-$\frac{1}{\sqrt{{S}_{n+1}}}$),
∴Tn<2[($\frac{1}{\sqrt{{S}_{1}}}$-$\frac{1}{\sqrt{{S}_{2}}}$)+…+($\frac{1}{\sqrt{{S}_{n}}}$-$\frac{1}{\sqrt{{S}_{n+1}}}$)]=2($\frac{1}{\sqrt{{S}_{1}}}$-$\frac{1}{\sqrt{{S}_{n+1}}}$)=2($\sqrt{2}$-$\sqrt{\frac{n+2}{n+1}}$)<2($\sqrt{2}$-1).
点评 本题考查数列的通项,考查不等式的证明,考查放缩法的运用,正确放缩是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l∥β | D. | 若l∥α,l⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
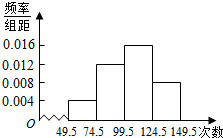 为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.
为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com