
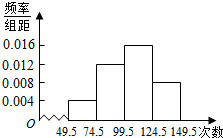
 为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.
为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.分析 (1)根据频率和为1,求出第四小组的频率;
(2)根据频率=$\frac{频数}{样本容量}$求出该班级的学生人数n;
(3)求出各小组的频数,即可得出学生阅读时间的中位数落在第几小组.
解答 解:(1)第四小组的频率为
1-(0.1+0.3+0.4)=0.2;
(2)设该班级的学生人数是n,
则n=20÷0.4=50;
(3)因为0.1×50=5.0,
0.3×50=15,
0.2×50=10;
所以第一、第二、第三、第四小组的频数分别为5、15、20和10;
所以学生阅读时间的中位数落在第三小组内.
点评 本题考查了频率分布直方图的应用问题,也考查了频数、频率与样本容量的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
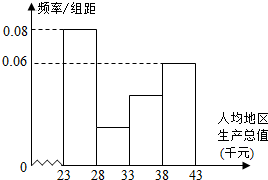 据我国西部各省(区、市)2013年人均地区生产总值(单位:千元)绘制的频率分布直方图如图所示,则人均地区生产总值在区间[28,38)上的频率是( )
据我国西部各省(区、市)2013年人均地区生产总值(单位:千元)绘制的频率分布直方图如图所示,则人均地区生产总值在区间[28,38)上的频率是( )| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{2}$-y2=1 | B. | ${x^2}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要 | B. | 必要而不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
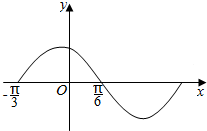 函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,如果x1,x2∈(-$\frac{π}{3}$,$\frac{π}{6}$),且f(x1)=f(x2),则f(x1+x2)等于( )
函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,如果x1,x2∈(-$\frac{π}{3}$,$\frac{π}{6}$),且f(x1)=f(x2),则f(x1+x2)等于( )| A. | -1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com