Question

2．若定义在R上的函数f（x）满足f（-x）=f（x），f（2-x）=f（x），且当x∈[0，1]时，f（x）=$\sqrt{1-x^2}$，则函数H（x）=|xe^x|-f（x）在区间[-5，1]上的零点个数为6．

Answer 1

分析 求出函数m（x）=xe^x的导函数，由导函数等于0求出x的值，以求出的x的值为分界点把原函数的定义域分段，以表格的形式列出导函数在各区间段内的符号及原函数的增减性，从而得到函数的单调区间及极值点，把极值点的坐标代入原函数求极值．然后判断y=|xe^x|的极值与单调性，然后推出零点的个数．

解答 解：定义在R上的函数f（x）满足f（-x）=f（x），f（2-x）=f（x），
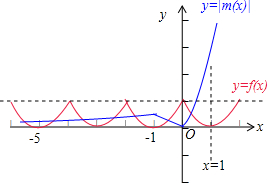
∴函数f（x）是偶函数，且函数的图象关于x=1对称．
∵函数m（x）=xe^x的定义域为R，m′（x）=（xe^x）′=x′e^x+x（e^x）′=e^x+xe^x，
令m′（x）=e^x+xe^x=e^x（1+x）=0，解得：x=-1．
列表：

x	（-∞，-1）	-1	（-1，+∞）
m′（x）	-	0	+
m（x）	↓	极小值	↑

由表可知函数m（x）=xe^x的单调递减区间为（-∞，-1），单调递增区间为（-1，+∞）．
当x=-1时，函数m（x）=xe^x的极小值为m（-1）=-$\frac{1}{e}$．
故函数y=|xe^x|在x=-1时取得极大值为$\frac{1}{e}$，
且y=|xe^x|在（-∞，-1）上是增函数，在（-1，-∞）上是减函数，
在区间[-5，1]上，故当x＜0时，y有5个交点，当x＞0时，y有1个交点，共有6个交点，
如图所示：

故答案为：6．

点评 本题考查了利用导数研究函数的单调性与极值，在求出导函数等于0的x值后，借助于表格分析能使解题思路更加清晰，此题是中档题．