
分析 (1)化简$n{a_{n+1}}=(n+1){a_n}+n(n+1),n∈{N^*}$可得$\frac{{{a_{n+1}}}}{n+1}=\frac{a_n}{n}+1$,从而写出$\frac{a_n}{n}=λ+n-1$,即${a_n}={n^2}+(λ-1)n$;
(2)当λ=2时,an=n2+n,从而求得bn=2n,从而求等比数列前n项和.
(3)仿照(2)可得${a_n}={n^2}+(λ-1)n$,bn=$\sqrt{2}$2n+r-2,从而化简cn=$\sqrt{2}$2-r-2n-($\frac{1}{{n}^{2}+(λ-1)n}$),从而分类讨论以确定λ的值.
解答 解:(1)证明:∵$n{a_{n+1}}=(n+1){a_n}+n(n+1),n∈{N^*}$,
两边除以n(n+1)得,$\frac{{{a_{n+1}}}}{n+1}=\frac{a_n}{n}+1$,
即$\frac{{{a_{n+1}}}}{n+1}-\frac{a_n}{n}=1$,故数列$\{\frac{a_n}{n}\}$为等差数列,
故$\frac{a_n}{n}=λ+n-1$,故${a_n}={n^2}+(λ-1)n$;
(2)当λ=2时,an=n2+n,
∵${b_1}{b_2}…{b_n}={(\sqrt{2})^{a_n}}$,
∴b1=${\sqrt{2}}^{2}$=2,
bn+1=$\frac{{b}_{1}{b}_{2}{b}_{3}…{b}_{n}{b}_{n+1}}{{b}_{1}{b}_{2}…{b}_{n}}$=$\frac{{\sqrt{2}}^{(n+1)^{2}+n+1}}{{\sqrt{2}}^{{n}^{2}+n}}$=2n+1,
综上所述,bn=2n,
Sn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2;
(3)仿照(2)可得,
${a_n}={n^2}+(λ-1)n$,bn=$\sqrt{2}$2n+r-2,
cn=$\frac{{a}_{n}-{b}_{n}}{{a}_{n}{b}_{n}}$=$\frac{1}{{b}_{n}}$-$\frac{1}{{a}_{n}}$=$\sqrt{2}$2-r-2n-($\frac{1}{{n}^{2}+(λ-1)n}$),
∵对一切n∈N*,均有T4≥Tn恒成立,
∴当n>4时,cn≤0;
若λ=1,则cn=$\sqrt{2}$1-2n-$\frac{1}{{n}^{2}}$,
c5=$\frac{1}{16\sqrt{2}}$-$\frac{1}{30}$>0,故T5>T4,故不成立;
若λ=2,则cn=$\sqrt{2}$-2n-$\frac{1}{n(n+1)}$,
故c1=$\frac{1}{2}$-$\frac{1}{2}$=0,c2=$\frac{1}{4}$-$\frac{1}{6}$,c3=$\frac{1}{8}$-$\frac{1}{12}$>0,c4=$\frac{1}{16}$-$\frac{1}{20}$>0,
c5=$\frac{1}{32}$-$\frac{1}{30}$<0,
且当n≥5时,2n>n2+n,
故成立;
若λ=3,则cn=$\frac{1}{\sqrt{2}•{2}^{n}}$-$\frac{1}{{n}^{2}+2n}$,
故c1=$\frac{1}{2\sqrt{2}}$-$\frac{1}{3}$>0,c2=$\frac{1}{4\sqrt{2}}$-$\frac{1}{8}$>0,c3=$\frac{1}{8\sqrt{2}}$-$\frac{1}{15}$>0,c4=$\frac{1}{16\sqrt{2}}$-$\frac{1}{24}$>0,
故且当n≥5时,$\sqrt{2}$•2n>n2+2n,故成立;
若λ≥4,则cn=$\frac{1}{{\sqrt{2}}^{r-2}•{2}^{n}}$-$\frac{1}{{n}^{2}+(r-1)n}$,
c4=$\frac{1}{{\sqrt{2}}^{r-2}16}$-$\frac{1}{16+4(r-1)}$,
令f(r)=16${\sqrt{2}}^{r-2}$-16-4(r-1),
则f′(r)=16•ln$\sqrt{2}$•${\sqrt{2}}^{r-2}$-4=4(ln4•${\sqrt{2}}^{r-2}$-1)>0,
故f(r)在[4,+∞)上是增函数,
故f(4)=16×2-16-4×3>0,
故c4<0,
故T3>T4,故不成立;
综上所述,λ的值为2或3.
点评 本题考查了等比经数列与等差数列的性质的判断与应用,同时考查了导数的综合应用及分类讨论的思想与方程思想,函数思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
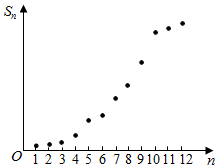 某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )
某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )| A. | 7 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | z<32? | B. | z<258? | C. | z<34? | D. | z<260? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{λ}{4}$ | B. | $\frac{λ}{2}$ | C. | λ | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com