
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是在区间[-1,0]上任取两个数x和y,写出事件对应的集合,做出面积,满足条件的事件是y<3x,写出对应的集合,做出面积,得到概率.
解答 解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[-1,0]上任取两个数x和y,对应的面积是sΩ=1,
满足条件的事件是y<3x,事件对应的集合是A={(x,y)|-1≤x≤0,-1≤y≤0,y<3x}
对应的图形的面积是sA=$\frac{1}{2}×\frac{1}{3}×1$=$\frac{1}{6}$,
∴根据等可能事件的概率得到P=$\frac{1}{6}$
故选:A.
点评 本题考查等可能事件的概率,是一个几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到结果,是一个中档题.


科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
| 需要量(万件) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
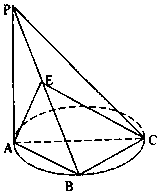 如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点.
如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (-∞,-3) | C. | (-∞,3] | D. | (-∞,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com