
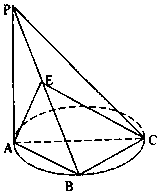
 如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点.
如图,点B是以AC为直径的圆周上的一点,PA=AB=BC,AC=4,PA⊥平面ABC,点E为PB中点.分析 (Ⅰ)证明BC⊥面PAC,推出BC⊥AE,然后证明AE⊥PB,推出AE⊥平面PBC,然后证明平面AEC⊥平面PBC.
(Ⅱ)作BO⊥平面APC,取PO的中点G,连结EG,连结AG,说明∠EAG就是直线AE与平面PAC所成角,通过解三角形求解即可.
解答 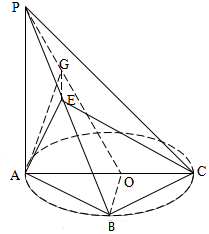 (Ⅰ)证明:∵PA⊥⊙O所在平面,且BC为⊙O的弦,
(Ⅰ)证明:∵PA⊥⊙O所在平面,且BC为⊙O的弦,
∴PA⊥BC
∵AB为⊙O的直径,
∴BC⊥AC.
而PA∩AC=A.
∴BC⊥面PAC,
∵AE?平面PAC,∴BC⊥AE,
∵PA=AB,PA⊥平面ABC,点E为PB的中点.
∴AE⊥PB,PB∩BC=B,
∴AE⊥平面PBC.
∵AE?平面AEC,
∴平面AEC⊥平面PBC.
(Ⅱ)解:作BO⊥平面APC,取PO的中点G,连结EG,
则EG∥BO,⇒EG⊥平面PAC,连结AG,
∴∠EAG就是直线AE与平面PAC所成角,
AE=$\frac{1}{2}$PB=2,GE=$\frac{1}{2}OB$=1,
∴sin∠EAG=$\frac{GE}{AE}$=$\frac{1}{2}$,
∴直线AE与平面PAC所成角为:$\frac{π}{6}$.
点评 本题考查的知识点是直线与平面垂直的判定,直线与平面所成角的求法,其中熟练掌握空间线面垂直、平行的判定、性质,善于根据直角三角形、圆周角的性质,判断出直线与直线垂直是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| P(K2≥k) | … | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | … |
| k | … | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | … |
| A. | 90% | B. | 95% | C. | 97.5% | D. | 99.5% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| B. | 在线性回归分析中,回归直线不一定过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 | |
| D. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
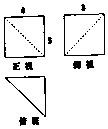 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com